  |
| Politica de confidentialitate |
|
|
| • domnisoara hus • legume • istoria unui galban • metanol • recapitulare • profitul • caract • comentariu liric • radiolocatia • praslea cel voinic si merele da aur | |
Vectori si valori proprii - exercitii rezolvate
1. Calculati valorile si vectorii proprii pentru matricile:
a) ![]() ; b)
; b) 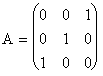
2. Stabiliti daca matricile de la exercitiul precedent se pot diagonaliza si, in caz afirmativ, scrieti forma lor diagonala.
3. Consideram aplicatia ![]() ,
,![]() .
.
a) Verificati daca T este transformare liniara.
b) Scrieti matricea atasata lui T, ![]() .
.
c) Calculati valorile si vectorii proprii
atasati lui ![]() .
.
d) Scrieti subspatiile proprii corespunzatoare transformarii T si stabiliti daca aceasta se poate diagonaliza.
e) Scrieti, daca exista, matricea diagonalizatoare C si matricea diagonala D.
B) REZOLVARI
1. a) Construim polinomul caracteristic, ![]() .
.
![]()
Deci, ![]() . Rezolvam ecuatia caracteristica,
. Rezolvam ecuatia caracteristica, ![]() , adica
, adica ![]() si obtinem radacinile
si obtinem radacinile
![]() ,
,
care sunt valorile proprii corespunzatoare matricii A.
Vectorul propriu corespunzator valorii proprii ![]() : cautam
: cautam ![]() , v de forma
, v de forma ![]() , pentru care
, pentru care ![]() . Inlocuim si obtinem:
. Inlocuim si obtinem:
![]()
![]()
Atunci, 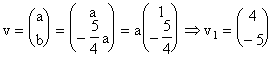 este vectorul propriu
corespunzator valorii proprii
este vectorul propriu
corespunzator valorii proprii ![]() .
.
Vectorul propriu corespunzator valorii proprii ![]() : cautam
: cautam ![]() , v de forma
, v de forma ![]() , pentru care
, pentru care ![]() . Inlocuim si obtinem:
. Inlocuim si obtinem:
![]()
![]()
Atunci, ![]() este vectorul propriu
corespunzator valorii proprii
este vectorul propriu
corespunzator valorii proprii ![]() .
.
b) Construim polinomul caracteristic, ![]() .
.
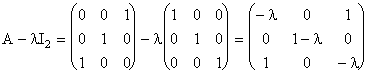
Deci, ![]() . Rezolvam ecuatia caracteristica,
. Rezolvam ecuatia caracteristica, ![]() , de unde obtinem radacinile:
, de unde obtinem radacinile:
![]() ,
,
care sunt valorile proprii corespunzatoare matricii A.
Vectorul propriu corespunzator valorii proprii ![]() : cautam
: cautam ![]() , v de forma
, v de forma 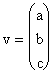 , pentru care
, pentru care ![]() . Inlocuim si obtinem:
. Inlocuim si obtinem:
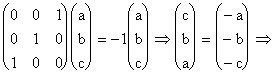
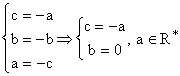
Atunci, 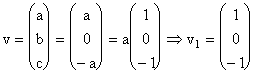 este vectorul propriu
corespunzator valorii proprii
este vectorul propriu
corespunzator valorii proprii ![]() .
.
Vectorul propriu corespunzator valoriilor proprii egale ![]() : cautam
: cautam ![]() , v de forma
, v de forma 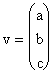 , pentru care
, pentru care ![]() . Inlocuim si obtinem:
. Inlocuim si obtinem:
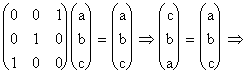
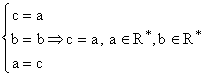
Atunci, 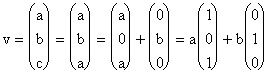 . Deci vectorul propriu corespunzator valoriilor proprii
egale
. Deci vectorul propriu corespunzator valoriilor proprii
egale ![]() este o combinatie
liniara de vectorii
este o combinatie
liniara de vectorii  .
.
2. Studiem daca matricea ![]() este diagonalizabila:
valorile proprii pe care le-am obtinut sunt
este diagonalizabila:
valorile proprii pe care le-am obtinut sunt ![]() , ambele cu ordin de multiplicitate egal cu 1 in ecuatia
caracteristica, deci
, ambele cu ordin de multiplicitate egal cu 1 in ecuatia
caracteristica, deci ![]() . Vectorii proprii genereaza urmatoarele subspatii proprii:
. Vectorii proprii genereaza urmatoarele subspatii proprii:
![]()
![]()
Deci, A se poate diagonaliza si forma ei diagonala este
![]()
Pentru matricea 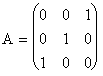 , valorile proprii sunt
, valorile proprii sunt
![]() ,
,
cu ordinele de multiplicitate ![]() si
si ![]() . Vectorii proprii genereaza urmatoarele subspatii proprii:
. Vectorii proprii genereaza urmatoarele subspatii proprii:
![]()
Pentru ![]() , dimensiunea o vom putea determina abia dupa ce vom studia
liniar independenta vectorilor
, dimensiunea o vom putea determina abia dupa ce vom studia
liniar independenta vectorilor ![]() . Fie B matricea construita cu acesti doi vectori,
. Fie B matricea construita cu acesti doi vectori, 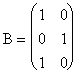 . Un calcul simplu arata ca ea are rangul 2, egal cu numarul
de vectori din care a fost construita. Deci,
. Un calcul simplu arata ca ea are rangul 2, egal cu numarul
de vectori din care a fost construita. Deci, ![]() sunt liniar
ndependenti si deci
sunt liniar
ndependenti si deci ![]() .
.
Prin urmare, si pentru cazul b) de la exercitiul 1, matricea A este diagonalizabila. Forma ei diagonala este:
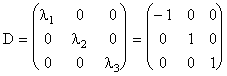
3. a) Aratam ca T este transformare liniara.
Fie ![]() si fie
si fie ![]() . Aratam ca
. Aratam ca
![]()
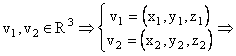
![]()
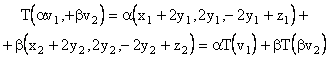
Deci, aplicatia T este aplicatie liniara.
b) Matricea atasata aplicatiei T este 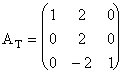 .
.
c) Calculam valorile si vectorii proprii ai
lui ![]() .
.
Construim polinomul caracteristic, ![]()
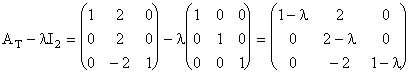
Deci, ![]() . Rezolvam ecuatia caracteristica,
. Rezolvam ecuatia caracteristica, ![]() , de unde obtinem radacinile:
, de unde obtinem radacinile:
![]() ,
,
care sunt valorile proprii corespunzatoare matricii A, cu ordinele de
multiplicitate ![]() si
si ![]() .
.
Vectorul propriu corespunzator valorilor proprii egale ![]() : cautam
: cautam ![]() , v de forma
, v de forma 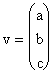 , pentru care
, pentru care ![]() . Inlocuim si obtinem:
. Inlocuim si obtinem:
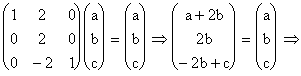
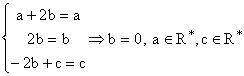
Atunci, 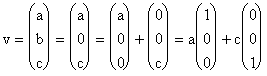 . Deci, vectorul propriu corespunzator valorilor proprii
egale
. Deci, vectorul propriu corespunzator valorilor proprii
egale ![]() este o combinatie
liniara de vectorii
este o combinatie
liniara de vectorii 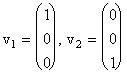 .
.
Vectorul propriu corespunzator valorii proprii ![]() : cautam
: cautam ![]() , v de forma
, v de forma 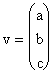 , pentru care
, pentru care ![]() . Inlocuim si obtinem:
. Inlocuim si obtinem:
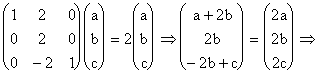
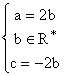
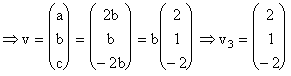
este vectorul propriu corespunzator valorii proprii ![]() .
.
d) Subspatiile proprii sunt: ![]() si
si ![]() . Evident,
. Evident, ![]() .
.
Pentru a determina ![]() , studiem liniar independenta vectorilor
, studiem liniar independenta vectorilor ![]() si
si ![]() . Matricea construita cu ajutorul acestor doi vectori este
. Matricea construita cu ajutorul acestor doi vectori este 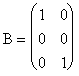 si are rangul doi, egal cu numarul de vectori din care a fost
construita. Atunci,
si are rangul doi, egal cu numarul de vectori din care a fost
construita. Atunci, ![]() .
.
Prin urmare, matricea ![]() si implicit
transformarea T sunt diagonalizabile. Matricea diagonala este
si implicit
transformarea T sunt diagonalizabile. Matricea diagonala este 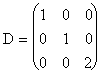 , iar matricea diagonalizatoare este
, iar matricea diagonalizatoare este 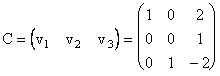 .
.
C) PROBLEME PROPUSE PENTRU AUTOEVALUARE
1. Calculati valorile si vectorii proprii pentru matricile:
a) ![]() ; b)
; b) ![]() ; c)
; c) 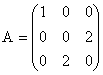 ; d)
; d) 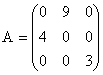
2. Stabiliti daca matricile de la exercitiul precedent se pot diagonaliza si, in caz afirmativ, scrieti forma lor diagonala.
3. Consideram aplicatia ![]() ,
,![]() .
.
f) Verificati daca T este transformare liniara.
g) Scrieti matricea atasata lui T, ![]() .
.
h) Calculati valorile si vectorii proprii
atasati lui ![]() .
.
i) Scrieti subspatiile proprii corespunzatoare transformarii T si stabiliti daca aceasta se poate diagonaliza.
j) Scrieti, daca exista, matricea diagonalizatoare C si matricea diagonala D.
|
|