Spatii vectoriale - exercitii rezolvate

1. Verificati ca structura algebrica este spatiu vectorial.

2. Aratati ca vectorii de mai jos sunt liniar independenti:

a) , , in

b) , ,  in

c) , , in

3. Aratati ca vectorii urmatori sunt liniar dependenti si stabiliti relatia de dependenta.

a) , , , in .

b) , , in

c) , , , in

4. Determinati valoarea parametrului real m pentru care vectorii de mai jos sunt liniar dependenti: , , , in

5. Verificati ca urmatoarea multime este subspatiu vectorial al lui

B) REZOLVARI

1. Va trebui sa verificam, pe rand, cele 6 axiome ale spatiului vectorial.

Av1. , are loc .

Fie , . Atunci, bazandu-ne pe proprietatea de asociativitate a adunarii numerelor reale, avem succesiv:

++=

=, ceea ce trebuia demonstrat.

Av2. , dat de , astfel incat are loc :

Axioma este verificata imediat:

.

Av3. .

.

Av4. si , are loc

.

Av5. si

, . Atunci:

Av6. si , are loc .

.

Cele sase axiome fiind verificate, putem spune ca este spatiu vectorial.

2. a) Conform definitiei pentru liniar independenta, consideram combinatia liniara . Vom arata ca . Prin inlocuirea vectorilor, obtinem:

.

Obtinem sistemul:

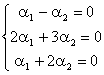    (S)

Sistemul obtinut este un sistem omogen, deoarece termenul liber este nul. El admite, deci, solutia , fapt care se verifica imediat prin inlocuire directa. Pentru ca vectorii sa fie liniar independenti este necesar ca aceasta solutie sa fie si unica. Matricea sistemului este: 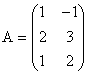, cu rangul 2 deoarece: ; ; . Din sistemul (S) mentinem primele doua ecuatii, corespunzatoare liniilor minorului .

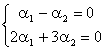
Deoarece , acest sistem are determinantul nenul, deci are solutie unica. Deoarece este solutie, deducem ca ea este si singura. Ea verifica de asemenea si ecuatia a treia din sistemul (S), deci sistemul (S) are ca unica solutie pe . Atunci, vectorii sunt liniar independenti.

b) Procedam la fel ca la punctul a) si, din inlocuirea in obtinem sistemul:

   

La fel ca si sistemul (S) de al punctul anterior, este un sistem omogen, care admite solutia . Matricea sistemului este 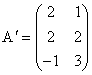si are rangul egal cu 2 deoarece ; ; . Din primele doua ecuatii ale sistemului obtinem:

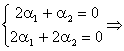
solutie unica.

Aceasta verifica de asemenea si ecuatia a treia a lui , deci este solutie unica pentru egalitatea . Atunci, vectorii dati sunt liniar independenti.

c) Pornim cu combinatia liniara , de unde prin inlocuirea vectorilor si efectuarea calculelor obtinem sistemul:

  

Matricea sistemului este 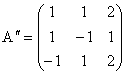si are determinantul nenul, deci rangul trei. Deoarece matricea are determinantul nenul, sistemul are solutie unica. Dar, pentru ca este sistem omogen, aceasta solutie unica este si vectorii sunt liniar independenti.

Observatie importanta: Pentru fiecare punct al problemei rezolvate anterior, matricile sistemelor care apar, sunt construite cu ajutorul vectorilor dati in enunt, asezati pe coloana. In fiecare caz in parte, rangul matricii a fost egal cu numarul de vectori dati. Se poate enunta o regula de lucru, care isi are justificarea riguroasa in teoria sistemelor de ecuatii liniare si in definitia liniar independentei:

REGULA 1: Fie , vectori de dimensiune n. Daca matricea construita cu ajutorul acestor m vectori asezati pe coloana are rangul m, atunci vectorii sunt liniar independenti.

Sa mentionam ca matricea poate fi construita si cu vectorii asezati pe linii. Regula ramane si in acest caz valabila.

Conventie: In continuare, daca nu se vor face alte precizari, de fiecare data cand ne vom referi la matricea construita cu ajutorul unor vectori, vom sti ca vectorii au fost asezati pe coloana.

O consecinta imediata a regulii 1 este enuntata in continuare si va fi utilizata la exercitiul 3.

Consecinta: Daca rangul matricii construite cu ajutorul vectorilor este mai mic decat m, atunci vectorii sunt liniar dependenti.

3. a) Construim matricea A, cu ajutorul celor trei vectori:

; ;

. Deci, rangA este o valoare diferita de numarul de vectori (ei sunt in numar de trei). Din consecinta enuntata anterior, deducem ca sunt liniar dependenti. Pentru determinarea relatiei de dependenta trebuie sa efectuam calculele in . Ca urmare a inlocuirilor, se obtine sistemul:

,

a carui matrice este matricea A pe care am scris-o anterior. Mentinem ca necunoscute principale pe , corespunzatoare in matricea A coloanelor care formeaza minorul nenul si notam . Atunci:

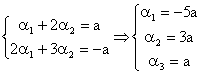
Prin urmare, combinatia liniara se scrie:

b) Se observa imediat, fara a mai fi necesare calcule, ca . Aceasta egalitate arata ca sunt liniar dependenti, precum si relatia dintre ei.

c) Construim matricea formata cu cei trei vectori:

:; ; .

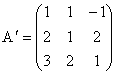Deoarece rangul matricii A rezulta a fi 2 si nu este egal cu numarul de vectori dati, deducem ca sunt liniar dependenti. Pentru a determina relatia de dependenta, consideram combinatia liniara . Dupa inlocuiri, rezulta sistemul:

, cu matricea 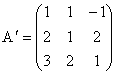, al carei rang egal cu 2 este dat de minorul . Notam variabila secundara si mentinem primele doua ecuatii din sistem.

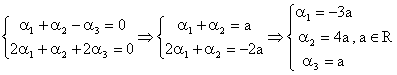
Atunci, devine: si relatia de dependenta se scrie: .

4. Cu ajutorul vectorilor dati, putem construi o matrice patratica de dimensiune trei:

Conditia ca vectorii sa fie liniar dependenti este, conform consecintei la regula 1, ca rangul lui A sa fie mai mic decat 3. Altfel spus, conditia se scrie , deci .

5. Conform definitiei subspatiului vectorial, avem de aratat ca:

si , avem

Din (1)

Din (2)

Dar (3)

Daca desfacem parantezele in (3) si dam factor comun pe si , acolo unde este posibil, obtinem:

=0,

ceea ce este adevarat, din (1) si (2). Am aratat, deci, ca si , avem , adica am dovedit ca este satisfacuta proprietatea impusa prin definitia subspatiului vectorial. Atunci, W este subspatiu vectorial al lui .

C) PROBLEME PROPUSE PENTRU AUTOEVALUARE

1. Verificati ca urmatoarele structuri algebrice sunt spatii vectoriale reale:

a) unde este multimea matricelor cu doua linii si doua coloane si elemente din R, iar + si . sunt, respectiv, adunarea si inmultirea matricilor.

b) , unde

, iar + si . sunt, respectiv, adunarea si inmultirea polinoamelor de gradul al doilea, cu coeficienti reali.

2. Verificati daca vectorii urmatori sunt liniar independenti. Acolo unde proprietatea nu este satisfacuta, stabiliti relatia de dependenta.

a) , , , in

b) , , , in .

c) , , , in .

d) , , , in .

e) , , , in

3. Pentru ce valoare a parametrului real m, vectorul  se poate scrie ca o combinatie liniara a vectorilor si ?

a) , , , in .

b) , , , in .

4. Verificati daca fiecare din multimile de mai jos formeaza subspatii vectoriale ale spatiilor indicate:

a), in .

b) , in