Sisteme de generatori, baze - exercitii rezolvate

1. Studiati daca sistemele de vectori de mai jos formeaza sistem de generatori in spatiile vectoriale din care fac parte:

a) , , in

b) , , in

c) , , , in

2. Verificati daca sistemele de vectori de mai jos formeaza baza in spatiile vectoriale din care fac parte:

a) , , , in

b) , , in

c) , , , in

3. Fie vectorii si , in . Gasiti un al treilea vector, , astfel ca multimea sa fie baza a lui .

4. Se dau multimile de vectori

si .

a) Aratati ca F si G reprezinta baze in

b) Scrieti coordonatele vectorilor in raport cu baza G

c) Construiti matricea de trecere de la baza F la baza G.

B) REZOLVARI

1. a) Fie ales arbitrar. Daca este sistem de generatori in , atunci exista constantele , cu proprietatea ca

(1)

Din , fie v de forma , cu arbitrar fixati. Inlocuind in egalitatea (1), obtinem:

Dupa efectuarea calculelor obtinem sistemul:

,

cu necunoscutele . Matricea sistemului este , cu determinantul egal cu 4, nenul. Sistemul admite, deci, solutie unica. Determinam valorile pentru si obtinem:

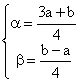
Deci, pornind de la vectorul arbitrar , de forma , cu arbitrar fixati, am gasit doua constante reale astfel incat v sa se poata scrie ca in (1) sau, mai explicit,

.

Aceasta egalitate arata ca vectorul v poate fi generat din vectorii si, cum v a fost ales arbitrar, deducem ca pot genera intreg spatiul .

b) Fie ales arbitrar, . Cautam constantele , cu proprietatea ca

(2)

Inlocuim si efectuam calculele. Obtinem urmatorul sistem:

, cu matricea .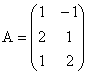

Matricea are rangul 2. Pentru rezolvarea sistemului, mentinem primele doua ecuatii si obtinem:

Deci, pornind de la combinatia liniara (2), am gasit valorile cautate . Totusi, pentru ca acestea sa fie solutii ale sistemului (S'), trebuie sa verifice si a treia ecuatie si anume . Inlocuind, obtinem:

Pe de alta parte, am presupus ca vectorul este arbitrar, ceea ce inseamna ca intre coordonatele lui nu trebuie sa existe o relatie restrictiva, de tipul in acest caz. Deducem de aici ca vectorii nu pot genera un vector oarecare al spatiului , deci nu formeaza sistem de generatori al acestui spatiu.

c) Fie ales arbitrar. Cautam , cu proprietatea ca

Dupa efectuarea calculelor obtinem sistemul:

,

cu necunoscutele si matricea sistemului , cu rangul egal cu 2.  Necunoscutele principale sunt , pe care le vom determina in functie de Sistemul (S) se scrie:

.

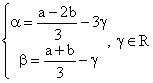Aceasta arata ca vectorul v poate fi generat din vectorii si, cum v a fost ales arbitrar, deducem ca pot genera intreg spatiul .

Observatii importante:

In rezolvarea tuturor celor trei subpuncte ale problemei 1, esential a fost sa dovedim existenta sau, dimpotriva, inexistenta coeficientilor combinatiei liniare din definitia sistemului de generatori.

La primul punct, coeficientii si ai combinatiei liniare (1) au fost determinati ca unica solutie a sistemului (S). Acest sistem este de tip Cramer, el avand determinantul nenul. Matricea sistemului este formata cu vectorii asezati pe coloane si are rangul 2, egal cu numarul coordonatelor vectorilor .

La cel de-al doilea punct, matricea sistemului (S') rezultat din combinatia liniara (2) are rangul 2, mai mic decat numarul de coordonate ale vectorilor . In acest caz, am aratat ca nu formeaza sistem de generatori.

La punctul al treilea, matricea sistemului are rangul egal cu numarul componentelor fiecaruia dintre vectorii si acestia s-au dovedit a fi sistem de generatori in .

Se poate enunta o regula generala, a carei justificare se afla in teoria sistemelor liniare.

Regula 2: Daca rangul matricii construite cu vectorii , asezati pe linii sau pe coloane, este diferit de n, atunci vectorii dati nu formeaza sistem de generatori in spatiul din care fac parte.

2. a) Reamintim ca, prin definitie, un sistem de vectori formeaza baza daca el satisface in acelasi timp proprietatile de liniar independenta si sistem de generatori. Putem aborda problema prin calcul direct, verificand efectiv cele doua proprietati, sau putem face o sinteza intre Regula 1 din tema 3 si regula 2 enuntata anterior:

Fie, deci, un sistem de vectori si fie matricea formata cu acesti vectori asezati pe coloana.

Regula 1 spune ca sunt liniar independenti daca

Regula 2 spune ca sunt sistem de generatori pentru spatiul , daca .

Pentru ca ambele conditii sa fie indeplinite, trebuie ca . Dar, odata ce , matricea A devine matrice patratica, iar conditia inseamna de fapt . Putem enunta acum o a treia regula, dupa care vom trece la rezolvarea efectiva a exercitiului 2.

Regula 3: Fie sistemul de vectori . Acesta formeaza o baza in , daca matricea formata cu cei trei vectori asezati pe linii sau pe coloane are determinantul nenul.

Revenind la punctul a) al problemei 2, matricea obtinuta cu ajutorul vectorilor asezati pe coloana, de exemplu, este:

.

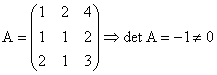Conform cu regula 3, reprezinta o baza in .

b) Matricea construita cu ajutorul celor doi vectori dati nu este o matrice patratica:

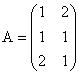
Vectorii nu formeaza, prin urmare, o baza in .

c) matricea nefiind patratica, vectorii nu formeaza o baza in .

3. Aplicand regula trei, deducem imediat ca trebuie sa alegem un vector astfel incat matricea construita cu ajutorul vectorilor dati, si a acestui al treilea vector, , sa aiba determinantul nenul. Fie, de exemplu, . Matricea care se obtine este:

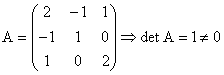
deci cu aceasta alegere a lui , multimea devine baza a lui .

Observatie: Alegerea lui de mai sus este doar una dintre multele alegeri pe care le putem face. De exemplu, daca , obtinem

.

Daca , obtinem:

.

In ambele cazuri, sistemul de vectori este o baza a lui . De fapt, intr-un spatiu vectorial exista o infinitate de posibilitati de alegere a unei baze. Singurele elemente de acre trebuie tinut cont sunt:

Ø      Matricea construita cu ajutorul vectorilor alesi sa fie patratica

Ø      Determinantul ei sa fie nenul

Revenind la problema 3, observam ca intotdeauna vectorii dintr-o baza a lui vor fi in numar de trei: ei au, fiecare, cate trei componente si pentru ca matricea construita cu ajutorul lor sa fie patratica, avem nevoie de exact trei vectori. Putem afirma ca toate bazele din spatiul vectorial si, in general, , au acelasi numar de elemente: trei, respectiv n.

4.

si

a) F si G sunt baze in .

Construim matricile:

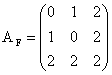si ,

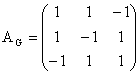pentru care calculam determinantii: , . Deoarece valorile acestor determinanti sunt nenule, F si G reprezinta baze in .

b) Sa facem observatia ca F si G fiind baze in , vectorii reprezinta sistem de generatori ai acestui spatiu. Deci, orice vector v din admite o scriere in functie de acesri vectori, de forma:

cu unic determinate din R. Prin urmare, si vectorii admit, fiecare in parte, o astfel de scriere si anume:

Vom spune atunci ca sunt coordonatele vectorului in baza G, scriind . Analog, pentru ceilalti doi vectori din F.

Pentru determinarea efectiva a coordonatelor, inlocuim in (1), (2) si (3) vectorii cunoscuti. Dupa efectuarea calculelor obtinem urmatoarele sisteme de ecuatii:

, ,

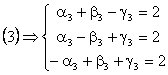
Rezolvarea lor va conduce la determinarea coordonatelor vectorului in baza G. Totusi, pentru rezolvarea acestor sisteme ar trebui sa depunem un volum mare de munca si de aceea vom aborda o varianta mai simpla. Sa observam, pentru inceput, ca matricea atasata celor trei sisteme de mai sus este aceeasi. Practic, aceste sisteme difera doar prin termenii lor liberi, care sunt transcrierea pe coloana a vectorilor , adica vectorii transpusi. In plus, matricea celor trei sisteme este exact 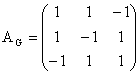. Cu aceste observatii, scriem: ,,

Utilizand inversa matricii , aceste trei relatii se scriu:

, ,    (4)

Rezolvarea problemei s-a redus, asadar, la calculul matricii inverse . Utilizand metoda eliminarii complete (tema 2), obtinem:

Calculand fiecare din cei trei vectori dati in (4), obtinem:

, ,

c) Matricea de trecere de la baza F la baza G o vom nota si este formata din exprimarea vectorilor in baza G. Mai exact,

.

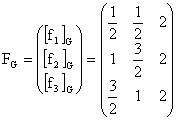C) PROBLEME PROPUSE PENTRU AUTOEVALUARE

1. Stabiliti daca sistemele de vectori de mai jos formeaza sistem de generatori in spatiile vectoriale din care fac parte:

a) , , in

b) , , in

c) , , in

d) , , in

e) , , in

f) , , , in

2. Care dintre sistemele de vectori de la exercitiul 1 formeaza o baza in spatiul vectorial din care fac parte?

3. Fie vectorii , din . Gasiti un al treilea vector, , astfel ca multimea sa fie baza a lui .

4. Consideram familiile de vectori 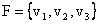, unde sunt vectorii de la exercitiul 3 si .

a) Aratati ca G este o baza in

b) Scrieti coordonatele vectorilor in raport cu baza G

c) Construiti matricea de trecere de la baza F la baza G si apoi de la baza G la baza F.