Serii - exerctii rezolvate

1. Studiati natura urmatoarelor serii, apoi gasiti suma lor, calculand limita sirului sumelor partiale :

a); b); c); d)

Studiati natura seriilor urmatoare, utilizand criteriul raport ului:

a)    b) c) d) e)

B) REZOLVARI

1. a) Termenul general al seriei este .

Sirul sumelor partiale are termenul general

Aducem la o forma echivalenta, utilizand procedeul de descompunere in fractii simple:

Deci . Prin urmare,

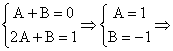
Deoarece , seria data este convergenta si are suma .

b) Termenul general al seriei este . Sirul sumelor partiale are termenul general

Aducem la o forma echivalenta, utilizand procedeul de descompunere in fractii simple:

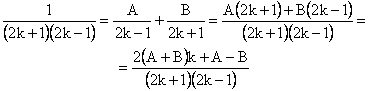
Deci . Prin urmare,

Deoarece , seria data este convergenta si are suma .

c) Termenul general al seriei este . Sirul sumelor partiale are termenul general

Aducem la o forma echivalenta, utilizand procedeul de descompunere in fractii simple:

Deci . Prin urmare,

Deoarece , seria data este convergenta si are suma .

d) Termenul general al seriei este . Sirul sumelor partiale are termenul general

Aducem la o forma echivalenta, astfel:

Prin urmare,

Deoarece , seria data este convergenta si are suma .

2. a) Avem de calculat , unde:

Atunci , deci seria este convergenta.

b) Calculam , unde:

Atunci , deci seria este divergenta.

c) 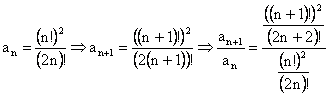, adica

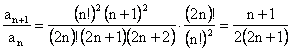
Atunci , deci seria este convergenta.

d)

Atunci , deci seria este convergenta.

e)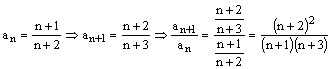

Atunci , deci  nu putem stabili natura seriei utilizand acest criteriu.

C) PROBLEME PROPUSE PENTRU AUTOEVALUARE

1. Studiati natura urmatoarelor serii, apoi gasiti suma lor, calculand limita sirului sumelor partiale

a)    b) c) d) e)

Studiati natura seriilor urmatoare, utilizand criteriul raport ului:

a)    b) c) d) e) f)