Serii alternate

1. Studiati natura urmatoarelor serii alternate, stabilind daca ele sunt convergente si absolut convergente:

a)     b) c) d)

B) REZOLVARI

1. a)

Termenul general al seriei alternate este . Convergenta seriei date este asigurata daca sunt indeplinite conditiile criteriului lui Le ibniz, adica :

i)  este monoton descrescator:

Din , deci  este monoton descrescator.

ii) .

Ambele conditii fiind indeplinite, seria alternata este convergenta.

Studiem absolut convergenta ei si pentru aceasta consideram seria modulelor,

,

care este o serie cu termeni pozitivi si pentru care termenul general este . Seria data in exercitiu este absolut convergenta daca  seria modulelor este convergenta. Pentru studiul naturii seriei aplicam criteriul raportului.

,

prin urmare seria modulelor este convergenta, deci seria alternata este absolut convergenta.

Sa facem observatia ca pentru aceasta serie era suficient sa studiem absolut convergenta pentru a stabili si convergenta ei, deoarece stim ca, daca o serie alternata este absolut convergenta, atunci ea este si convergenta. Pentru seriile de la punctele b)-d)  vom studia converganta utilizand criteriul lui Leibniz doar daca ele nu se vor dovedi absolut convergente.

b)

Consideram seria modulelor,

,

care este o serie cu termeni pozitivi si pentru care termenul general este .

Studiem convergenta  seriei modulelor si aplicam criteriul raportului.

,

prin urmare seria modulelor este convergenta, deci seria alternata este absolut convergenta. Absolut convergenta ne asigura ca seria alternata este si convergenta.

c)

Seria modulelor este: , serie cu termeni pozitivi si pentru care termenul general este .

Studiem convergenta  seriei modulelor si aplicam criteriul raportului.

,

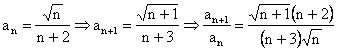
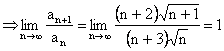prin urmare nu putem stabili natura seriei modulelor utilizand criteriul raportului. Aplicam criteriul Raabe-Duhamel si calculam

deci seria modulelor nu este convergenta si prin urmare seria alternata nu este absolut convergenta. In aceasta situatie va trebui sa studiem convergenta seriei alternate utilizand criteriul lui Leibniz.

Termenul general al seriei alternate este . Convergenta seriei date este asigurata daca sunt indeplinite conditiile criteriului lui Le ibniz, adica :

i)  este monoton descrescator:

Din

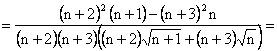
daca , deci  este monoton descrescator.

ii) .

Ambele conditii fiind indeplinite, seria alternata este convergenta.

d)

Seria modulelor este , cu termenul general  . Suma partiala de ordinul n este

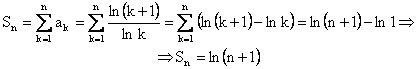
Deci, . Seria modulelor nu este convergenta si deci seria alternata nu este absolut convergenta. Studiem daca sunt indeplinite cele doua conditii din criteriul lui Leibniz, pentru convergenta seriei alternate:

i)  este monoton descrescator:

Din .

Atunci,

Sirul  se dovedeste astfel a fi crescator si prima conditie din criteriul Leibniz este incalcata. Deci, seria alternata din enunt nu este nici convergenta, nici absolut convergenta.

C) PROBLEME PROPUSE PENTRU AUTOEVALUARE

1. Studiati natura urmatoarelor serii alternate, stabilind daca ele sunt convergente si absolut convergente:

a)   

b)   

c)   

d)