Produs scalar - exercitii rezolvate

1. Stabiliti care dintre urmatoarele operatii determina produs scalar pe spatiile vectoriale precizate:

a)     , .

b)     , .

c)     , .

d)    , si .

2. Calculati lungimea vectorilor si de mai jos, unghiul dintre ei si proiectia lui pe , utilizand produsele scalare indicate, de la exercitiul anterior:

a)    , , in cu 1a).

b)    , , in cu 1d).

3. Utilizand determinantul Gramm, studiati liniar independenta vectorilor urmatori:

a)    , , in .

b)    , , , in .

c)    , , ,  in .

B) REZOLVARI

1. a) Verificam ca sunt satisfacute conditiile celor trei axiome ale produsului scalar:

a1)

,

ceea ce trebuia demonstrat.

a2)

,

ceea ce trebuia demonstrat.

a3)

,

ceea ce trebuia demonstrat.

Prin urmare, conditiile din cele trei axiome sunt indeplinite, deci operatia data este produs scalar pe .

b) Verificam de asemenea cele trei axiome:

a1)

ceea ce trebuia demonstrat.

a2)

ceea ce trebuia demonstrat.

a3)

Pentru de exemplu, se observa ca , deci a treia axioma nu este verificata.

Operatia data in acest caz nu este un produs scalar.

c) a1)

ceea ce trebuia demonstrat.

a2)

ceea ce trebuia demonstrat.

a3)

Pentru de exemplu, se observa ca si a treia axioma nu este verificata.

Deci, operatia data nu este un produs scalar.

d) a1)

ceea ce trebuia demonstrat.

a2)

,

ceea ce trebuia demonstrat.

a3)

,

ceea ce trebuia demonstrat.

Prin urmare, conditiile din cele trei axiome sunt indeplinite, deci operatia data este produs scalar pe .

2. a)

Deci,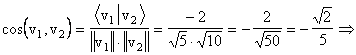

unghiul dintre vectorii si este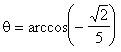

Proiectia cautata este .

b)

Deci,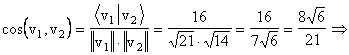

unghiul dintre vectorii si este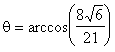

Proiectia cautata este .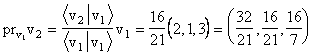

3. a) Calculam urmatoarele produse scalare:

Determinantul Gramm este:

,

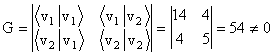deci vectorii sunt liniar independenti.

b) Calculam urmatoarele produse scalare:

Determinantul Gramm este:

,

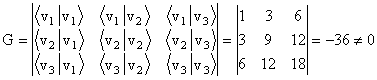deci vectorii sunt liniar independenti.

c) Calculam urmatoarele produse scalare:

Determinantul Gramm este:

,

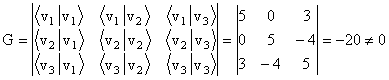deci vectorii sunt liniar independenti.

C) PROBLEME PROPUSE PENTRU AUTOEVALUARE

1. Stabiliti care dintre urmatoarele operatii determina produs scalar pe spatiile vectoriale precizate:

a)     , .

b)     , .

c)    , si .

2. Calculati lungimea vectorilor si de mai jos, unghiul dintre ei si proiectia lui pe , utilizand produsele scalare indicate, de la exercitiul anterior:

a)    , , in cu 1a).

b)    , , in cu 1c).

3. Utilizand determinantul Gramm, studiati liniar independenta vectorilor urmatori:

a)    , , in .

b)    , , , in .

c)    , , ,  in .