OPERATII CU VECTORI

Fie vectorii intre care exista relatiile:

λ - scalar; λ ≠ 0

Cat poate fi λ, astfel incat vectorii si sa fie coliniari:

REZOLVARE:    

Se obtine sistemul:

Eliminand pe m, obtinem:

ec. de gradul II

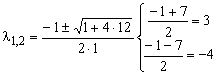
Obtinem solutiile:

a.       b.

Se considera paralelipipedul din figura. Sa se scrie sub forma analitica vectorii: .

Se dau lungimile muchiilor: OA=2; OB=4; OC=3

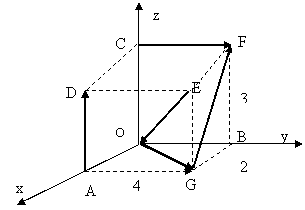
REZOLVARE

=

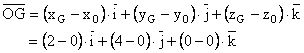
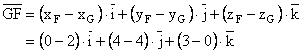
Sa se calculeze produsul scalar al vectorilor:

REZOLVARE:    

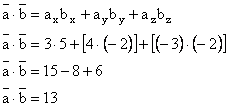
Care este unghiul facut de vectorii:

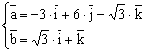
REZOLVARE:    

Sa se calculeze produsul vectorial al vectorilor:

REZOLVARE:    

Se considera cubul OABCDEFG avand muchiile

OA = OC = OD si vectorii .

Sa se calculeze produsele vectoriale:

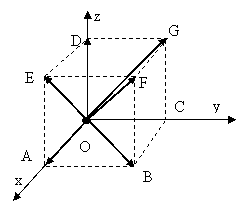
REZOLVARE:    

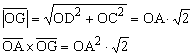
Se sa sistemul de forte din figura de mai jos:

, , , ,

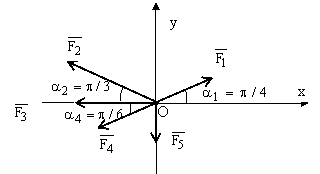
Se cer:

1. Suma proiectiilor fortelor pe axa Ox;
2. Suma proiectiilor fortelor pe axa Oy;
3. Rezultanta sistemului de forte ;
4. Unghiul format de cu axa Ox (a

REZOLVARE:    

a.

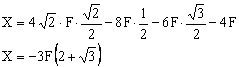
b.

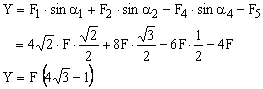
c.

d.

8. Se da sistemul de forte din figura de mai jos:

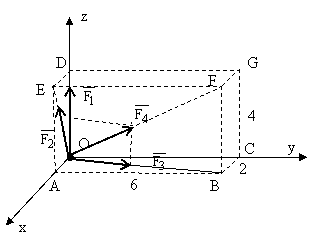
Sa se determine:

a.       Suma proiectiilor fortelor pe axele Ox, Oy, Oz (X, Y, Z);

b.      Rezultanta fortelor ;

c.       Pozitia rezultantei fortelor (a

REZOLVARE:    

a.

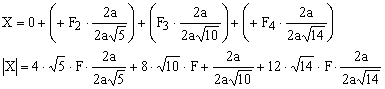
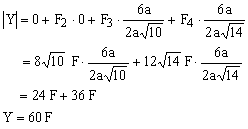
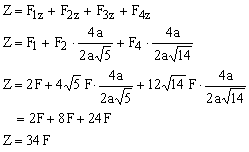
b.

c.

PROBLEME PROPUSE SPRE REZOLVARE

Se dau vectorii:

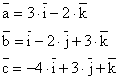
Se cer:

a.

b. cosinusii directori ai lui

c.

d.

Pentru sistemele de forte din figurile a,b, se dau: ;

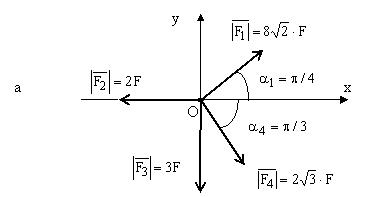Se cer:  a.

b.

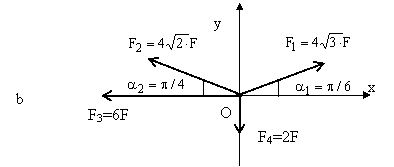
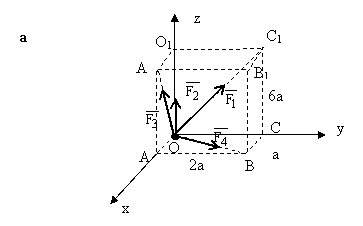
Date: a, F, directiile lui F_i din figura si , , ,

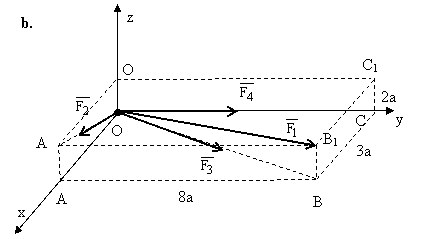
Date: , , ,

Se cer: a. expresiile analitice ale fortelor:

b. expresia rezultantei , a modulului .