  |
| Politica de confidentialitate |
|
|
| • domnisoara hus • legume • istoria unui galban • metanol • recapitulare • profitul • caract • comentariu liric • radiolocatia • praslea cel voinic si merele da aur | |
Exercitii matrice - rezolvate
1. Dati exemplu de o matrice si gasiti un model concret care sa se poata scrie restrans cu ajutorul ei.
2. Se dau matricile 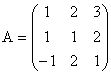 ;
; 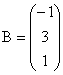 ;
; 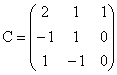
a) Stabiliti dimensiunea matricilor date
b) Calculati: 2A, AB, AC, 3A - 4C.
c) Calculati detA si detC si stabiliti daca matricile A si C sunt inversabile.
3) Se da matricea 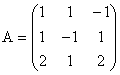
a) Calculati detA
b) Construiti transpusa lui A, ![]()
c) Construiti matricea adjuncta, ![]()
d) Construiti inversa matricii A, ![]() , apoi verificati corectitudinea rezultatului obtinut
utilizand relatia
, apoi verificati corectitudinea rezultatului obtinut
utilizand relatia ![]() , unde
, unde ![]() este matricea unitate
cu trei linii si trei coloane.
este matricea unitate
cu trei linii si trei coloane.
4) Stabiliti daca sistemul de ecuatii de mai jos este compatibil, apoi calculati valorile necunoscutelor utilizand urmatoarele metode de rezolvare: reducere, substitutie, metoda matriceala si metoda Cramer.
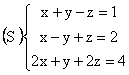
5) Determinati rangul matricilor de mai jos:
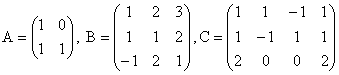
6) Rezolvati urmatoarele sisteme de ecuatii liniare:
a) 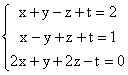 ; b)
; b) 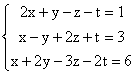
B) REZOLVARI
1. Fie matricea ![]() si modelul dat mai
jos:
si modelul dat mai
jos:
Intr-o institutie lucreaza 124 persoane, dintre care 47 sunt cu studii superioare. Repartizarea personalului dupa sex si forma de pregatire este data in tabelul de mai jos, unde cu S am notat *studii superioare*, iar cu M *studii medii*.
|
|
Femei |
Barbati |
|
S |
|
|
|
M |
|
|
Matricea A indica tocmai distributia personalului dupa criteriile din tabel.
2. a) Matricele A si C au cate trei linii si trei coloane deci au
dimensiunea ![]() . Mai putem spune ca A si C sunt matrici patratice si notam
. Mai putem spune ca A si C sunt matrici patratice si notam ![]() . Matricea B are trei linii si o singura coloana, deci are
dimensiunea
. Matricea B are trei linii si o singura coloana, deci are
dimensiunea ![]() . Putem nota aceasta prin
. Putem nota aceasta prin ![]() .
.
b)
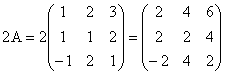 ;
; 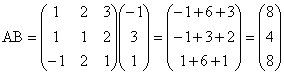 ;
;
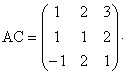
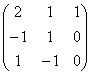
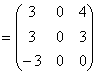
3A - 4C = 3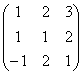 - 4
- 4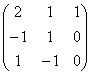 =
=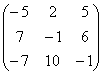
d) 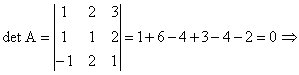 A nu este inversabila.
A nu este inversabila.
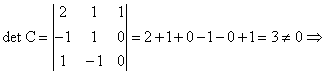 C este inversabila.
C este inversabila.
3) a) 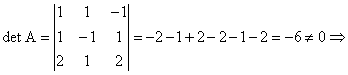 are sens inversa lui A.
are sens inversa lui A.
b) Matricea transpusa lui A este matricea care are drept coloane, liniile lui A:
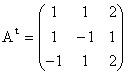
c) Matricea adjuncta are forma:

unde ![]() ,
, ![]() reprezentand
determinantul matricii care ramane dupa ce in matricea
reprezentand
determinantul matricii care ramane dupa ce in matricea ![]() au fost eliminate
linia i si coloana j.
au fost eliminate
linia i si coloana j.
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]()
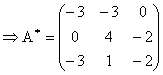
d) 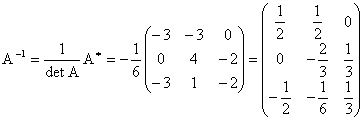
Verificarea prin calcul direct ca ![]() este imediata.
este imediata.
4. Matricea sistemului, 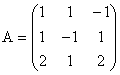 , este tocmai matricea pe care am intalnit-o la exercitiul
trei. Determinantul ei a fost calculat
si a rezultat o valoare nenula, ceea ce ne asigura ca sistemul are solutie si
aceasta este unica. Rezolvam sistemul prin metodele cerute:
, este tocmai matricea pe care am intalnit-o la exercitiul
trei. Determinantul ei a fost calculat
si a rezultat o valoare nenula, ceea ce ne asigura ca sistemul are solutie si
aceasta este unica. Rezolvam sistemul prin metodele cerute:
Metoda reducerii: Grupam ecuatiile doua cate doua si reducem necunoscuta z:
![]()
![]()
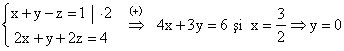
Din prima ecuatie a sistemului dat, obtinem ![]() .
.
Metoda substitutiei: Exprimam necunoscuta z din prima ecuatie si o inlocuim in ecuatiile doi si trei:

Metoda matriceala: Cu notatiile:
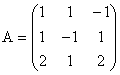 - matricea sistemului,
- matricea sistemului,
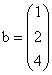 - vectorul termenilor
liberi,
- vectorul termenilor
liberi, 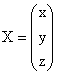 - vectorul necunoscutelor, sistemul dat capata scrierea
matriceala:
- vectorul necunoscutelor, sistemul dat capata scrierea
matriceala:
![]()
Dar, matricea ![]() a fost calculata la
exercitiul 3, deci
a fost calculata la
exercitiul 3, deci
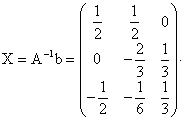
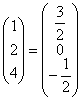
Metoda Cramer: Daca notam ![]() , atunci calculam necunoscutele x, z, z din formulele:
, atunci calculam necunoscutele x, z, z din formulele:
![]() ,
, ![]() ,
, ![]() ,
,
unde ![]() este determinantul
care se obtine inlocuind in
este determinantul
care se obtine inlocuind in ![]() coloana
corespunzatoare lui x cu termenul liber etc.
coloana
corespunzatoare lui x cu termenul liber etc.
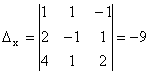 ;
; 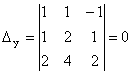 ;
; 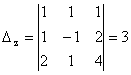
Deci, ![]() ,
, ![]() ,
, ![]() .
.
5. ![]()
Deoarece A este matrice patratica de dimensiune 2 si ![]() , rangul lui A va fi egal cu dimensiunea matricii, deci
, rangul lui A va fi egal cu dimensiunea matricii, deci ![]()
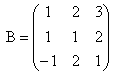
Deoarece B este matrice patratica de dimensiune 3 si ![]() , rangul lui B va fi mai mic decat dimensiunea matricii, deci
, rangul lui B va fi mai mic decat dimensiunea matricii, deci
![]()
![]() ;
; ![]() ;
; 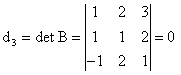
Deci, ![]() .
.
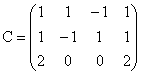
Deoarece matricea C nu este patratica, nu mai are sens calculul detC.
![]() ;
; ![]() ;
; 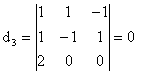
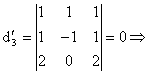
![]() este ultimul minor
nenul, deci
este ultimul minor
nenul, deci ![]() .
.
6. a) 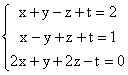
Sistemul are patru necunoscute si doar trei ecuatii. Matricea A atasata
sistemului, matricea extinsa ![]() si vectorul termenilor
liberi sunt:
si vectorul termenilor
liberi sunt:
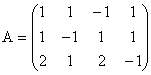 ;
; 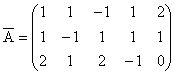 ;
; 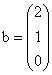
Conditia ca sistemul sa admita solutie este: ![]() . Calculam, deci, rangurile celor doua matrici:
. Calculam, deci, rangurile celor doua matrici:
Pentru ![]() :
:
![]() ;
; ![]() ;
; 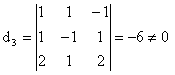
![]() .
.
Analog, obtinem ![]() , deci din egalitatea rangurilor celor doua matrici deducem
ca sistemul este compatibil. Deoarece elementele determinantului
, deci din egalitatea rangurilor celor doua matrici deducem
ca sistemul este compatibil. Deoarece elementele determinantului ![]() , care da rangul matricii A, corespund necunoscutelor x, z si
z din sistem, necunoscuta t este necunoscuta secundara si o notam
, care da rangul matricii A, corespund necunoscutelor x, z si
z din sistem, necunoscuta t este necunoscuta secundara si o notam ![]() . Sistemul se scrie:
. Sistemul se scrie:

![]() aplicam metoda Cramer.
aplicam metoda Cramer.
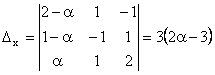 ;
; 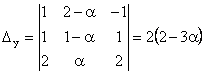 ;
;
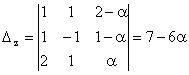 .
.
Deci, ![]() ,
, ![]() ,
, ![]() .
.
b) 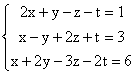
Matricea A atasata sistemului si matricea extinsa ![]() sunt:
sunt:
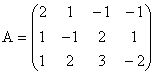 ;
; 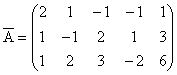 ;
;
Calculam rangurile celor doua matrici:
Pentru ![]() :
:
![]() ;
; ![]() ;
; 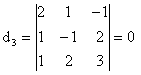 ;
;
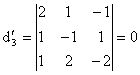
![]()
Pentru ![]() : minorii
: minorii ![]() se mentin identici ca
pentru calculul lui
se mentin identici ca
pentru calculul lui ![]() . Apare in plus:
. Apare in plus:
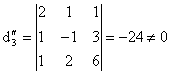
![]() ,
,
deci sistemul este incompatibil, deoarece ![]()
C) PROBLEME PROPUSE PENTRU AUTOEVALUARE
1. Se dau matricile 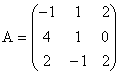 ,
, 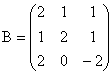 ,
, 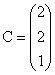 .
.
a) Stabiliti dimensiunea matricilor date.
b) Calculati ![]() .
.
c) Determinati valorile parametrilor a si b, pentru care are loc egalitatea
![]() , unde
, unde 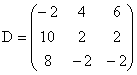 , iar
, iar ![]() este matricea unitate
cu trei linii si trei coloane.
este matricea unitate
cu trei linii si trei coloane.
d) Stabiliti daca A si B sunt matrici inversabile si, daca este cazul, calculati inversele lor.
e) Verificati corectitudinea rezultatelor obtinute la punctul d) utilizand
relatiile ![]() si
si ![]()
2) Sa se rezolve sistemul de ecuatii liniare:
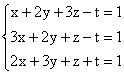
3) Determinati rangul matricilor de mai jos:
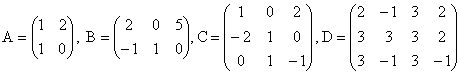
A) Sisteme de ecuatii
1. Rezolvati sistemele de ecuatii liniare de mai jos, utilizand metoda eliminarii complete:
a) 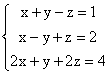 ; b)
; b) 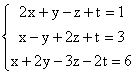
2. Construiti inversa matricii 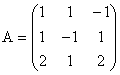 , utilizand metoda eliminarii complete. Comparati aceasta
metoda de lucru cu cea din rezolvarea exercitiului 3, seminar 1.
, utilizand metoda eliminarii complete. Comparati aceasta
metoda de lucru cu cea din rezolvarea exercitiului 3, seminar 1.
3. Utilizand transformari similare celor de la metoda eliminarii complete, sa se determine rangul matricilor:
a) 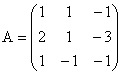 ; b)
; b)  ;c)
;c) 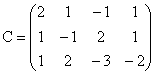
B) REZOLVARI
1.a) Matricea sistemului este 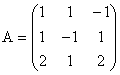 , pentru care
, pentru care ![]() . Deci, sistemul de ecuatii este compatibil determinat.
. Deci, sistemul de ecuatii este compatibil determinat.
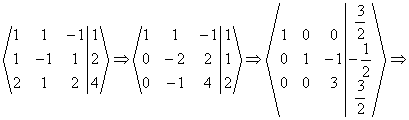
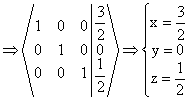 este solutia
sistemului.
este solutia
sistemului.
b) Matricea sistemului este 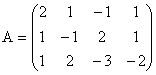 , iar matricea extinsa este
, iar matricea extinsa este 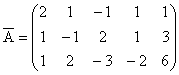 . Pentru a stabili daca sistemul este sau nu compatibil, calculam
. Pentru a stabili daca sistemul este sau nu compatibil, calculam
![]() si
si ![]() .
.
Pentru calculul ![]() :
:
![]()
![]() ,
, 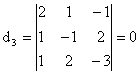 ,
,
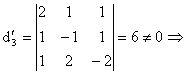
![]() =3.
=3.
Un calcul similar arata ca ![]() =3, deci sistemul este compatibil datorita egalitatii
rangurilor celor doua matrici. Notam
=3, deci sistemul este compatibil datorita egalitatii
rangurilor celor doua matrici. Notam ![]() , necunoscuta secundara. Sistemul se scrie:
, necunoscuta secundara. Sistemul se scrie: 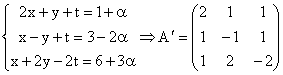 este matricea noului
sistem, pentru care
este matricea noului
sistem, pentru care ![]() . Deci, acest nou sistem are solutie pe care o putem
determina cu metoda eliminarii complete.
. Deci, acest nou sistem are solutie pe care o putem
determina cu metoda eliminarii complete.

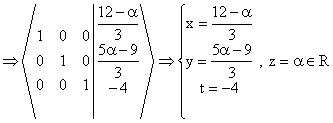 , este solutia
sistemului.
, este solutia
sistemului.
2. Construim un tablou asemanator celui de la rezolvarea sistemelor, dar de aceasta data in casuta a doua inscriem matricea unitate. Efectuam transformarile dupa regulile deja cunoscute, avand grija sa modificam atat elementele matricii A, cat si pe cele ale matricii unitate. In momentul in care in prima casuta am obtinut matricea unitate, in casuta a doua am obtinut inversa matricii A.
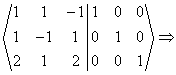
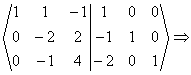
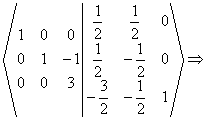
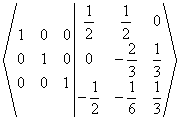
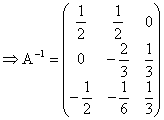
3. a) Pornim cu primul element al matricii pe pozitia pivotului:
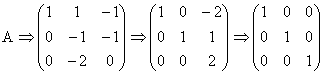
Deci, ![]() .
.
b) Cu acelasi prim element pe post de pivot, transformam matricea B:
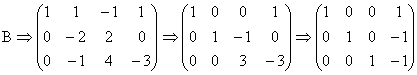
Deci, ![]()
c) Inainte de a incepe transformarile, permutam linia 1 cu linia 2 in matricea C pentru a aduce pe pozitia pivotului elementul 1.
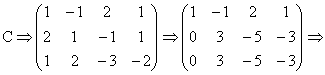
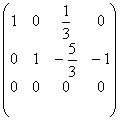 .
.
Calculele se opresc aici, deoarece urmatoarea alegere a pivotului ar trebui
sa fie 0. Prin urmare, ![]() .
.
C) PROBLEME PROPUSE PENTRU AUTOEVALUARE
1. Rezolvati sistemele de ecuatii de mai jos, utilizand metoda eliminarii complete:
a) 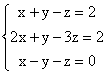 ; b)
; b) 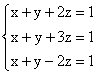 ;
;
c) 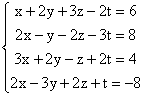 ; d)
; d) 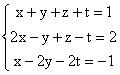
2. Utilizand metoda eliminarii complete, determinati inversele urmatoarelor matrici:
a) 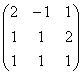 ; b)
; b) ![]() ; c)
; c) 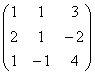
3. Determinati rangul matricilor de mai jos, utilizand metoda eliminarii complete:
a) ![]() ; b)
; b) ![]() ;
;
c) 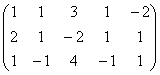 ; d)
; d) 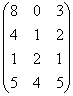
|
|