Diferentiale, puncte de extrem local

1. Calculati diferentiala de ordinul intai pentru functiile:

a)

b)

2. Determinati punctele de extrem local pentru urmatoarele functii:

a)

b)

B) REZOLVARI

1. a) Derivatele partiale de ordinul I sunt:

Atunci, diferentiala de ordinul intai este: , adica:

.

b) Derivatele partiale de ordinul I sunt:

Atunci, diferentiala de ordinul intai este: , adica:

.

2. a)

Calculam derivatele partiale de ordinul I.

Rezolvam sistemul de ecuatii:

.

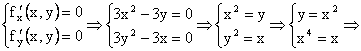
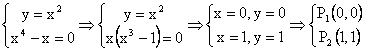Am obtinut astfel cele doua puncte stationare.

Calculam derivatele partiale de ordinul al doilea pentru functia f.

Matricea hessiana este:

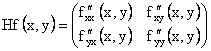
Pentru , avem: .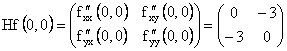

Deoarece , nu putem decide daca este punct de extrem sau nu.

Pentru , avem: .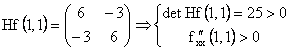

Deci, este punct de minim local, cu valoarea minima a functiei .

b)

Derivatele partiale de ordinul I sunt:

Rezolvam sistemul de ecuatii:

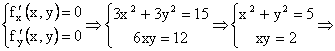
Am obtinut astfel patru puncte stationare , , , . Calculam derivatele partiale de ordinul al doilea pentru functia f.

Matricea hessiana este:

Pentru , avem:

.

Deoarece , punctul nu este punct de extrem .

c)

.

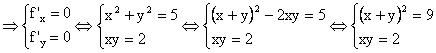
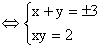
Construim matricea hessiana:

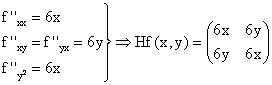
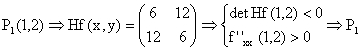, maxim.

C) PROBLEME PROPUSE PENTRU AUTOEVALUARE

Calculati diferentiala de ordinul I pentru functiile:

a)

b)

Determinati punctele de extrem local pentru urmatoarele functii:

a)

b)

c)

d)