Aplicatii liniare - exercitii rezolvate

1. Aratati ca aplicatia , data de  este aplicatie (transformare) liniara.

2. Care este proprietatea din definitia transformarii liniare, care nu este indeplinita de aplicatia , data de ?

3. Verificati liniaritatea aplicatiei ,

si apoi calculati rangul matricii atasate ei.

4. Fie matricea 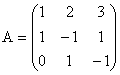. Construiti transformarea liniara  care are pe A ca matrice atasata si apoi determinati nucleul lui T.

5. Aflati daca transformarile liniare de la exercitiile 1 si 3 sunt aplicatii injective.

6. Studiati injectivitatea aplicatiei .

B) REZOLVARI

. Va trebui sa verificam ca este indeplinita proprietatea din definitia aplicatiei liniare:

Pe de alta parte,

Am obtinut, deci ca  si am aratat ca aplicatia T este liniara.

. Definitia transformarii liniare are la baza doua proprietati care trebuie sa fie indeplinite de aplicatia data.

a) Proprietatea de liniaritate:

 si

Deducem cu usurinta ca egalitatea  nu este indeplinita.

b) Proprietatea de omogenitate: .

De asemenea,

Este evident ca nici aceasta a doua proprietate nu este indeplinita.

. ,

Verificam proprietatea:

Se verifica imediat ca  deci ca aplicatia T este liniara.

Matricea atasata este

; ;

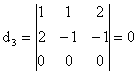
Deci, .

. Aplicatia  are forma: . Nucleul ei este , unde .

Fie . Atunci, , deci rezulta sistemul:

.

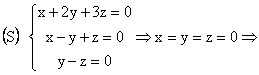
Din  deducem ca aplicatia T corespunzatoare matricii A este o aplicatie injectiva.

Observatie importanta: Sistemul omogen (S) la care s-a ajuns in rezolvarea problemei prin scrierea desfasurata a conditiei , are ca matrice a coeficientilor chiar matricea A din enuntul problemei. Determinantul acestei matrici este nenul, ceea ce asigura unicitatea sistemului (S). Deoarece (S) este un sistem omogen, aceasta unica solutie este cea nula, fapt care atrage dupa sine injectivitatea aplicatiei T. Putem desprinde de aici o regula de lucru si anume:

Regula 4: Daca matricea atasata unei transformari liniare este patratica si are determinantul nenul, atunci aplicatia este injectiva.

. a) Matricea atasata aplicatiei este 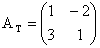. Aceasta este o matrice patratica, pentru care determinantul este egal cu 7, deci nenul. Din regula 4 deducea ca aplicatia data in problema este injectiva.

b) Matricea atasata transformarii este ., care nu mai este o matrice patratica. Deci, in absenta valorii determinantului (care nu are sens in acest caz) vom proceda la determinarea efectiva a nucleului aplicatiei.

, adica:

Matricea atasata sistemului este tocmai , pentru care am calculat deja rangul ca fiind 2. Mentinem necunoscutele principale x si y si fie . Sistemul se scrie:

.

Atunci, un element oarecare din nucleul aplicatiei T este

.

Deci, aplicatia T nu este aplicatie injectiva.

Fie . Atunci:

,

de unde deducem sistemul:

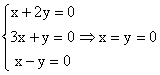 solutie unica.

Prin urmare,  si aplicatia este injectiva.

Observatie: Desi atat la exercitiul 5b cat si la 6, matricile atasate transformarilor liniare care apar sunt nepatratice, de dimensiuni , respectiv  si de rang 2, adica , totusi doar una dintre aplicatii este injectiva si anume cea din problema 6. Argumente solide, care isi au originea in teoria sistemelor liniare, ne ofera posibilitatea sa enuntam inca o regula.

Regula 5:  este aplicatie liniara injectiva daca si numai daca .

C) PROBLEME PROPUSE PENTRU AUTOEVALUARE

1. Verificati liniaritatea aplicatiilor de mai jos:

a) ,

b) ,

c) ,

d) ,

e) ,

f) ,

2. Construiti matricile atasate aplicatiilor pe care le-ati determinat a fi liniare in problema 1  si aflati rangul acestora.

3. Determinati nucleul fiecarei aplicatii liniare din exercitiul 1.

4. Care dintre matricile de mai jos pot fi atasate unor transformari liniare injective?

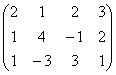a)  , b) , c)