OPERATII DE BAZA CU TABLOURI BIDIMENSIONALE

1. Citirea unei matrice

Se citeste numarul de linii si de coloane dupa care, in doua instructiuni FOR incluse una in cealalta, se citesc elementele matricei. Primul FOR parcurge cele n linii iar al doilea parcurge elementele de pe cate o linie.

write('Dati numarul de linii: ');

readln(n);

write('Dati numarul de coloane: ');

readln(m);

for i:=1 to n do

for j:=1 to m do

begin

write(' a[',i,',',j,']=');

readln(a[i,j]);

end

2. Afisarea unei matrice

Se folosesc doua instructiuni FOR. Pentru fiecare linie, se afiseaza elementele, pe rand si se trece la linia urmatoare de ecran.

for i:=1 to n do

begin

for j:=1 to m do

write(a[i,j],' ');

writeln;

end;

3. Parcurgere pe linii a matricei

Daca parcurgem elementele matricei pe linii, atunci le obtinem in ordinea: a₁₁, a₁₂, , a_1m, a₂₁, a₂₂, , a_2m, , a_n1, a_n2, , a_nm, unde n este numarul de linii iar m este numarul de coloane.

writeln('Matricea parcursa pe linii:');

for i:=1 to n do

for j:=1 to m do

write(a[i,j],' ');

4. Parcurgere pe coloane

Daca parcurgem elementele matricei pe coloane, atunci le obtinem in ordinea: a₁₁, a₂₁, , a_n1, a₁₂, a₂₂, , a_n2, , a_1m, a_2m, , a_nm , unde n este numarul de linii iar m este numarul de coloane.

writeln('Matricea parcursa pe coloane:');

for j:=1 to m do

for i:=1 to n do

write(a[i,j],' ');

5. Interschimbarea a doua linii

Data fiind o matrice cu n linii si m coloane, se cere sa se schimbe intre ele doua linii ale caror numere de ordine sunt date. Secventa de instructiuni cuprinde si validarea datelor si anume, numerele de linie p, respectiv q, sa fie cuprinse intre 1 si n (inclusiv) si sa nu coincida.

repeat

writeln('Dati liniile de interschimbat:');

readln(p,q);

until (p in [1..n]) and (q in [1..n]) and (p<>q);

for i:=1 to m do

begin

s:=a[p,i];

a[p,i]:=a[q,i];

a[q,i]:=s;

end;

6. Diagonala principala a unei matrice patratice

Daca elementele unei matrice patratice cu n linii si n coloane (numarul de linii este egal cu numarul de coloane) sunt:

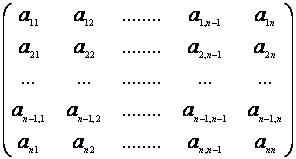, atunci diagonala principala contine elementele a₁₁, a₂₂, ., a_nn sau, mai pe scurt a_ii, cu i:=1,n. Parcurgerea acestora se face cu o singura instructiune for, ca in exemplul urmator:

writeln('Elementele diagonalei principale sunt: ');

for i:=1 to n do

write(a[i,i],' ');

7. Diagonala secundara a unei matrice patratice

In aceeasi matrice patratica de mai sus, diagonala secundara este formata din elementele: a_1n, a_2,n-1, a_3,n-2, , a_n-1,2, a_n,1. Deoarece fiecare dintre aceste elemente a_ij are suma indicilor i+j=n+1, diagonala secundara are elementele a_i,n-i+1, cu i=1, , n si este deci suficienta urmatoarea instructiune for pentru a o parcurge.

writeln('Elementele diagonalei secundare sunt: ');

for i:=1 to n do

write(a[i,n-i+1],' ');

8. Zona de deasupra diagonalei principale

((a_ij, i=1,n), j=i, n) -  inclusiv diagonala

((a_ij, i=1,n-1), j=i+1, n) -  fara diagonala

9. Zona de dedesubtul diagonalei principale

((a_ij, i=1,n), j=1, i) - inclusiv diagonala

((a_ij, i=2,n), j=1, i-1) - fara diagonala

10. Zona de deasupra diagonalei secundare

((a_ij, i=1,n), j=1, n-i+1) - inclusiv diagonala

((a_ij, i=1,n-1), j=1, n-i) - fara diagonala

11. Zona de dedesubtul diagonalei secundare.

((a_ij, i=1,n), j=n-i+1, n) - inclusiv diagonala

((a_ij, i=2,n), j=n-i+2, n) - fara diagonala