  |
| Politica de confidentialitate |
|
|
| • domnisoara hus • legume • istoria unui galban • metanol • recapitulare • profitul • caract • comentariu liric • radiolocatia • praslea cel voinic si merele da aur | |
OPERATII CU MATRICE - considerente matematice
1. Adunarea a doua matrice
Fie A si B doua matrice de tipul (n, m), adica A=![]() si B=
si B=![]() . Definim matricea C=
. Definim matricea C=![]() ale carei elemente sunt date de egalitatile cij=aij
+ bij, oricare ar fi i = 1, 2, ., n si j = 1, 2, ., m. matricea c se
numeste suma dintre matricele A si B si se noteaza C = A + B.
ale carei elemente sunt date de egalitatile cij=aij
+ bij, oricare ar fi i = 1, 2, ., n si j = 1, 2, ., m. matricea c se
numeste suma dintre matricele A si B si se noteaza C = A + B.
2. Inmultirea a doua matrice
Fie A = ![]() o matrice de tipul (n,
m) si B =
o matrice de tipul (n,
m) si B = ![]() de tipul (m, p).
Definim matricea C =
de tipul (m, p).
Definim matricea C = ![]() de tipul (n, p) ale
carei elemente sunt date de egalitatile:
de tipul (n, p) ale
carei elemente sunt date de egalitatile:
Cik = ai1b1k + ai2k2k
+ . + aimbmk = ![]() oricare ar fi i = 1,
2, ., n si k = 1, 2, ., p. Matricea C se numeste produ sul dintre A si B (in
aceasta ordine) si se noteaza C = AB. Operatia se numeste inmultire. Se observa
ca are sens sa vorbim de produsul matricei A cu matricea B (in aceasta ordine)
numai daca numarul de coloane ale lui A este egal cu numarul de linii ale
matricei B.
oricare ar fi i = 1,
2, ., n si k = 1, 2, ., p. Matricea C se numeste produ sul dintre A si B (in
aceasta ordine) si se noteaza C = AB. Operatia se numeste inmultire. Se observa
ca are sens sa vorbim de produsul matricei A cu matricea B (in aceasta ordine)
numai daca numarul de coloane ale lui A este egal cu numarul de linii ale
matricei B.
3. Transpusa unei matrice
Fie A = ![]() o matrice de tipul (n,
m). Matricea
o matrice de tipul (n,
m). Matricea ![]() unde taij
= aji, pentru orice i = 1, 2, ., m; j = 1, 2, ., n se numeste
transpusa matricei A. Se observa ca tA este o matrice de tipul (m,
n) si se obtine din A luand liniile, respectiv coloanele, lui A drept coloane,
respectiv linii, pentru tA (mai precis prima linie a lui tA este prima coloana a matricei A, a doua
linie a lui tA este a doua
coloana a lui A s. a. m. d.).
unde taij
= aji, pentru orice i = 1, 2, ., m; j = 1, 2, ., n se numeste
transpusa matricei A. Se observa ca tA este o matrice de tipul (m,
n) si se obtine din A luand liniile, respectiv coloanele, lui A drept coloane,
respectiv linii, pentru tA (mai precis prima linie a lui tA este prima coloana a matricei A, a doua
linie a lui tA este a doua
coloana a lui A s. a. m. d.).
In particular, daca A este o matrice patratica de ordinul n, atunci transpusa sa tA este de asemenea o matrice patratica de ordinul n. Daca i = j atunci taij = aji si deci diagonala principala a matricei tA este aceeasi cu diagonala principala a matricei A.
4. Determinanti de ordinul 2
Fie sistemul de doua ecuatii liniare cu doua necunoscute
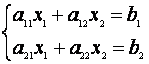 . Sa notam cu A
matricea coeficientilor sistemului, adica
. Sa notam cu A
matricea coeficientilor sistemului, adica 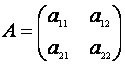 . A este o matrice patratica de ordinul doi.
. A este o matrice patratica de ordinul doi.
Rezolvarea acestui sistem este bine cunoscuta.
Aplicand metoda reducerii obtinem sistemul echivalent 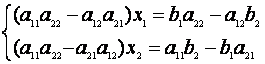 .
.
Presupunem ca a11a22 - a12a21 ¹ 0; atunci solutia sistemului este
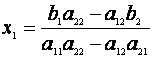 ,
, 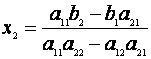 . Se observa ca numitorul din aceste egalitati se exprima simplu:
el este egal cu produsul elementelor de pe diagonala principala a matricei A
din care se scade produsul elementelor de pe diagonala secundara a matricei A.
. Se observa ca numitorul din aceste egalitati se exprima simplu:
el este egal cu produsul elementelor de pe diagonala principala a matricei A
din care se scade produsul elementelor de pe diagonala secundara a matricei A.
Acest numar se noteaza cu det A si se numeste determinantul matricei A, sau determinant de ordin doi (deoarece matricea A este de ordinul doi). Acest numar se noteaza de obicei si astfel:
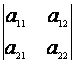 . Deci avem egalitatea
. Deci avem egalitatea 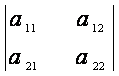 = a11a22 - a12a21.
In formulele care dau solutiile sistemului initial, se observa ca numaratorul
formulei care da valoarea lui x1 este tot un determinant de ordinul
doi, si anume determinantul matricei
= a11a22 - a12a21.
In formulele care dau solutiile sistemului initial, se observa ca numaratorul
formulei care da valoarea lui x1 este tot un determinant de ordinul
doi, si anume determinantul matricei 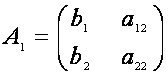 . Aceasta matrice se obtine din A inlocuind prima coloana din
A cu coloana formata din elementele b1 si b2. Analog, numaratorul formulei care da valoarea
lui x2 este un determinant de ordinul doi, si anume determinantul
matricei
. Aceasta matrice se obtine din A inlocuind prima coloana din
A cu coloana formata din elementele b1 si b2. Analog, numaratorul formulei care da valoarea
lui x2 este un determinant de ordinul doi, si anume determinantul
matricei  . Deci solutiile se
pot rescrie sub forma
. Deci solutiile se
pot rescrie sub forma 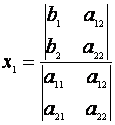 ,
, 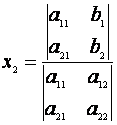 (*)
(*)
Formulele (*) poarta denumirea de formulele lui Cramer.
5. Determinanti de ordinul 3
Sa consideram acum un sistem de trei ecuatii liniare cu trei necunoscute.
 . Sa notam cu A matricea coeficientilor, adica
. Sa notam cu A matricea coeficientilor, adica
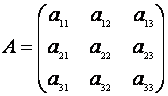 . Rezolvarea sistemului se face prin metoda reducerii. Daca
inmultim prima ecuatie cu a23 si a doua cu -a13 si le
adunam, obtinem ecuatia
. Rezolvarea sistemului se face prin metoda reducerii. Daca
inmultim prima ecuatie cu a23 si a doua cu -a13 si le
adunam, obtinem ecuatia
(a11a23 - a31a13)x1 + (a12a23 - a22a13)x2 = b1a23 - b2a13.
Analog, inmultim prima ecuatie cu a33 si a treia cu -a13 si apoi adunand, obtinem ecuatia:
(a11a33 - a31a13)x1 + (a12a33 - a32a13)x2 = b1a33 - b3a13.
Cu ecuatiile (1) si (2) formam un sistem cu doua ecuatii si doua necunoscute. Daca in acest sistem inmultim prima ecuatie cu a12a33 - a32a13 si a doua cu - (a12a23 - a22a13) si apoi le adunam, obtinem:
(3) (a11a22a33 + a12a23a31 + a13a21a 32 - a13a22a31 - a12a21a33 - a11a23a32)x1 = b1a22a33 + a12a23b3 + a13b2a32 - a13a22b3 - a12b2a33 - b1a23a32.
Numarul
care este coeficientul lui x1 in aceasta ecuatie il notam cu det A si il numim determinantul matricei A sau determinant
de ordin trei (deoarece matricea A este o matrice de ordinul trei). Acest
numar se noteaza de obicei si astfel:  .
.
In
ecuatia (3) se observa ca membrul doi este tot un determinant de ordinul trei si anume este determinantul
matricei de ordinul trei care se obtine din matricea A, matricea
coeficientilor, prin inlocuirea primei coloane cu coloana termenilor liberi din
sistem. Deci formula (3) se poate scrie astfel:  x1 =
x1 =  .
.
Procedand exact asa cum am facut pentru obtinerea ecuatiei (3), avem si ecuatiile care dau valorile lui x2 si x3:
 x2 =
x2 =  si
si  x3 =
x3 = 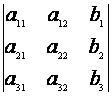 .
.
Daca
 ¹ 0 atunci valorile lui x1, x2 si x3
sunt:
¹ 0 atunci valorile lui x1, x2 si x3
sunt:
 ,
,  ,
, 
Aceste formule se numesc, de asemenea, formulele lui Cramer de rezolvare a sistemelor de trei ecuatii cu trei necunoscute.
APLICATIA
Programul urmator ilustreaza operatiile de baza cu matrice: suma si produsul a doua matrice, transpusa unei matrice, determinantii de ordinul doi si trei.
uses fdelay,crt;
type matrice=array[1..10,1..10] of integer;
var w:integer;
a,b:matrice;
procedure citire(var a:matrice;n,m:integer;c:char);
var i,j:integer;
begin
writeln;
for i:=1 to n do
for j:=1 to m do
begin
write(c,'[',i,',',j,']=');
readln(a[i,j]);
end
end;
procedure scrie(a:matrice;n,m:integer);
var i,j:integer;
begin
writeln;
for i:=1 to n do
begin
for j:=1 to m do
write(a[i,j]:5);
writeln;
end;
readln;
end;
procedure suma;
var c:matrice;
n,m,i,j:integer;
begin
clrscr;
write('Dati numarul de linii ale matricelor de adunat: ');
readln(n);
write('Dati numarul de coloane ale matricelor de adunat: ');
readln(m);
writeln('Dati prima matrice: ');
citire(a,n,m,'A');
writeln('Dati a doua matrice :');
citire(b,n,m,'B');
for i:=1 to n do
for j:=1 to m do
c[i,j]:=a[i,j]+b[i,j];
writeln;
writeln('Suma celor matrice este: ');
scrie(c,n,m);
end;
procedure produs;
var c:matrice;
n,m,p,k,i,j:integer;
begin
clrscr;
write('Dati numarul de linii ale primei matrice: ');
readln(n);
write('Dati numarul de coloane ale primei matrice: ');
readln(m);
write('Dati numarul de coloane ale matricei a doua: ');
readln(p);
writeln('Dati prima matrice: ');
citire(a,n,m,'A');
writeln('Dati a doua matrice :');
citire(b,m,p,'B');
for i:=1 to n do
for j:=1 to p do
begin
c[i,j]:=0;
for k:=1 to m do
c[i,j]:=c[i,j]+a[i,k]*b[k,j];
end;
writeln;
writeln('Produsul celor matrice este: ');
scrie(c,n,p);
end;
procedure transpusa;
var a,t:matrice;
n,m,i,j:integer;
begin
clrscr;
write('Dati numarul de linii ale matricei de transpus: ');
readln(n);
write('Dati numarul de coloane ale matricei de transpus: ');
readln(m);
writeln('Dati matricea: ');
citire(a,n,m,'A');
for i:=1 to n do
for j:=1 to m do
t[j,i]:=a[i,j];
writeln;
writeln('Matricea transpusa este: ');
scrie(t,m,n);
end;
procedure determinant2;
var a:matrice;
d:longint;
begin
clrscr;
writeln('Dati o matrice cu doua linii si doua coloane:');
citire(a,2,2,'A');
d:=a[1,1]*a[2,2]-a[2,1]*a[1,2];
write('Determinantul matricei este = ',d);
readln;
end;
procedure determinant3;
var a:matrice;
d:longint;
begin
clrscr;
writeln('Dati o matrice cu trei linii si trei coloane:');
citire(a,3,3,'A');
d:=a[1,1]*a[2,2]*a[3,3]+a[1,2]*a[2,3]*a[3,1]+a[1,3]*a[2,1]*a[3,2];
d:=d-a[1,3]*a[2,2]*a[3,1]-a[1,2]*a[2,1]*a[3,3]-a[1,1]*a[2,3]*a[3,2];
write('Determinantul matricei este = ',d);
readln;
end;
procedure meniu;
begin
clrscr;
writeln(' 1. SUMA A DOUA MATRICE');
writeln('
2. PRODUSUL A DOUA M
writeln(' 3. TRANSPUSA UNEI MATRICE');
writeln(' 4. DETERMINANT DE ORDIN DOI');
writeln(' 5. DETERMINANT DE ORDIN TREI');
writeln(' 6. TERMINARE PROGRAM');
writeln;
writeln('ALEGETI INTRE 1 SI 6');
end;
begin
repeat
repeat
meniu;
readln(W);
until (W>=1) and (W<=6);
case W of
1:SUMA;
2:PRODUS;
3:TRANSPUSA;
4:DETERMINANT2;
5:DETERMINANT3;
end;
until w=6;
end.
BIBLIOGRAFIE
1. C. Nastasescu, I. Stanescu, C. Nita - MATEMATICA, elemente de algebra superioara, manual pentru clasa a IX-a, E.D.P. - Bucuresti, 1999
2. T. Sorin, INFORMATICA, manual pentru clasa a IX-a, Ed. Infomat, -
Bucuresti, 1999
3. T. Sorin, INFORMATICA, manual pentru clasa a X-a, Ed. Infomat, -
Bucuresti, 1999
|
|