  |
| Politica de confidentialitate |
|
|
| • domnisoara hus • legume • istoria unui galban • metanol • recapitulare • profitul • caract • comentariu liric • radiolocatia • praslea cel voinic si merele da aur | |
Abordarea unei probleme in vederea elaborarii algoritmului de rezolvare. Exemple
In continuare, se vor expune etapele rezolvarii a doua probleme. Datele de intrare (DI) si datele de iesire (DE) se deduc din formularile problemelor. Aceste date vor fi precizate explicit dupa ce se dau indicatiile necesare pentru realizarea schemei logice (idei pentru gasirea algoritmului sau modul de organizare a datelor). De asemenea, vor fi precizate, acolo unde apar, datele intermediare (sau variabilele de lucru, VL), adica acele date care nu sunt nici de intrare, nici de iesire, dar sunt necesare pentru descrierea algoritmului.
Anumite variabile poarta denumiri specifice, care deriva din rolul lor. Printre acestea, vom regasi pe parcursul lucrarii:
contorii (variabilele contor). Denumirea vine din limba engleza (to count = a numara) si deci rolul lor este de 'a numara' (elementele cu o anumita proprietate, pasii dintr-o structura repetitiva etc.);
variabilele indicator. In engleza, se numesc 'flag variables' (flag = steag). O astfel de variabila poate lua doua valori (de obicei 1 sau 0, true sau false, dar orice pereche de valori distincte se poate folosi), astfel incat indica o situatie printr-o valoare si situatia contrara prin cealalta valoare. De exemplu, 1 inseamna ca vectorul este ordonat, 0 inseamna ca nu este ordonat; sau: true inseamna ca o functie f intoarce valori intregi, false inseamna ca f intoarce valori neintregi. Semnificatia valorilor unei variabile indicator, precum si rolul sau, trebuie precizate de programator.
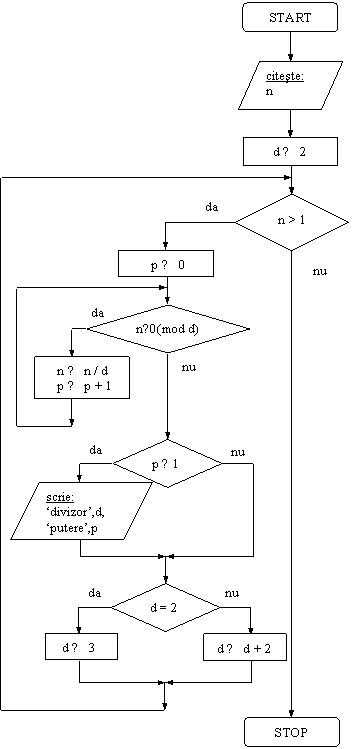
Exemplul 1. Se da n≥4, numar natural. Sa se scrie descompunerea sa in factori primi.
Mai intai vom analiza problema si astfel vom remarca ce variabile sunt necesare pentru descrierea unui algoritm care sa o rezolve. Se considera numarul natural n cel putin egal cu 4, intrucat cazurile n=1, n=2, n=3 sunt banale si in plus, considerarea lor ar complica inutil algoritmul (deseori astfel de cazuri particulare ale datelor de intrare presupun teste suplimentare si un tratament special). Stim ca n admite o descompunere de forma
n
=![]()
unde di, i=1,2,.,r sunt divizorii primi ai lui n si pi sunt puterile la care acestia apar. Vom propune o varianta de rezolvare in care, dupa ce se gaseste o pereche (di,pi) formata din divizor si putere, aceasta pereche este imediat afisata. Aceasta inseamna ca sunt suficiente doua variabile, pe care le vom numi d (divizor) si p (putere), ce vor pastra pe rand divizorii lui n si puterile corespunzatoare.
Sa analizam acum schema logica propusa mai jos. Astfel, dupa citirea lui n, variabila d se initializeaza cu 2, cel mai mic divizor prim posibil (a initializa o variabila inseamna a-i atribui, intr-un proces de prelucrare, o prima valoare; aceasta prima valoare se alege cu grija, analizand procesul ce urmeaza a fi dezvoltat). Urmeaza un proces repetitiv (remarcam sageata care se intoarce in punctul (1). Astfel, atata timp cat valoarea variabilei n se mentine mai mare decat 1, se repeta urmatoarea secventa de prelucrari:
variabila p primeste valoarea 0. Ideea este ca abia atunci cand d se gaseste ca este divizor al lui n, valoarea lui p sa devina 1;
un nou proces repetitiv. Cat timp n se imparte exact la d, se repeta secventa urmatoare:
n se imparte la d;
p creste cu 1.
La acest pas se determina puterea la care divizorul d apare in n;
daca p este mai mare decat 0, se afiseaza, in blocul de iesire marcat cu (2), valorile variabilelor d (divizorul) si p (puterea la care apare d in descompunerea lui n). Daca p nu este mai mare decat 0, atunci d nu divide n si se merge la (3);
daca divizorul testat a fost 2, atunci se va cerceta d=3. Altfel, variabila d se creste cu 2, caci stim ca numerele prime sunt impare (cu exceptia lui 2). Practic, se vor cerceta cazurile d=2, apoi d=3, 5, 7,. (pana unde este cazul).
Atunci cand testul (1) devine fals (ceea ce inseamna ca n=1) ne oprim, descompunerea fiind afisata. In final, nu dispunem in memorie de toti divizorii lui n iar valoarea lui n este alterata (n=1). Daca dorim sa pastram divizorii pentru prelucrari ulterioare, este necesar sa abordam altfel problema. De exemplu, am putea:
sa folosim un tablou in care sa memoram divizorii si puterile lor, in locatii succesive. Bunaoara, pentru n=175=52∙71, iesirea ar putea fi vectorul desc, desc = (5 2 7 1), sau
sa folosim doua tablouri, in primul sa memoram divizorii iar in al doilea, pe pozitii corespondente, puterile la care acestia apar. Pentru cazul de mai sus, iesirea ar fi vectorii d si p, d = (5 7), p = (2 1).
Observam ca exista mai multe posibilitati de a rezolva o problema (corespunzator necesitatilor de prelucrare a datelor respective) si ca ramane la alegerea programatorului sa propuna forma in care sa fie furnizate rezultatele.
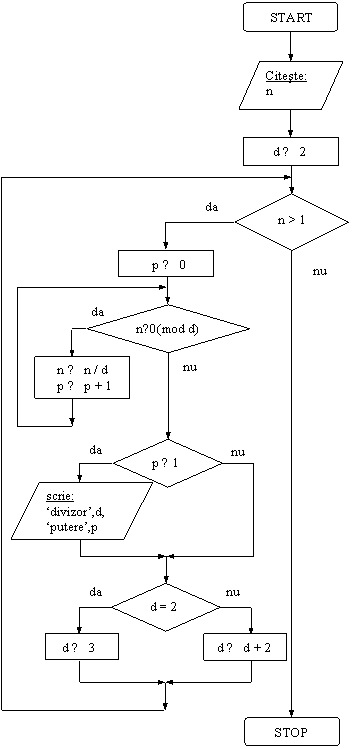 DI: variabila n
DI: variabila n
VL: -
DE: variabilele d, p.
(1)
(2)
(3)
Cum putem verifica daca am construit o schema logica corecta (si deci, un algoritm corect) pentru o problema propusa? Intai se verifica structurile repetitive, pentru a nu cicla la infinit. Apoi se verifica structurile alternative, sa furnizeze corect alegeri. Apoi se verifica daca toate variabilele folosite primesc valori pe parcursul schemei.
Daca toate verificarile indica o schema corecta, se trece la testul de birou. Aceasta este o metoda simpla, ce foloseste un tablou in care se plaseaza, pe coloane, toate variabilele ce apar in schema logica. Se aleg valori convenabile pentru datele de intrare - convenabile in sensul ca, pentru aceste date, vom rezolva problema:
direct;
urmarind, de la START la STOP, toti pasii indicati de schema logica
si vom compara rezultatele obtinute prin cele doua metode. Reluand procesul pentru mai multe seturi de date de intrare, vom observa daca algoritmul propus este corect (daca pentru macar un set de valori de intrare, raspunsul furnizat de schema nu coincide cu cel gasit direct, inseamna ca exista erori de logica si acestea trebuie corectate).
Pentru problema analizata aici, fie urmatorul tablou:
|
n |
d |
p |
Observatii |
|
|
|
|
|
|
|
|
|
se scriu 2 (d) si 1 (p) |
|
|
|
|
revenire in (1) |
|
|
|
|
p primeste din nou valoarea 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
se scriu 7 (d) si 2 (p) |
|
|
|
|
stop, n nu este > 1 |
Urmariti liniile tabloului de mai sus, urmand pas cu pas operatiile indicate de schema logica pentru n = 98. Se vede ca se obtine un rezultat corect (descompunerea 98 = 21∙72). Pentru orice valoare n ≥ 4, raspunsul este corect.
Este bine de stiut ca un astfel de tablou de variatie a variabilelor ne poate ajuta in constructia unui algoritm. Sa presupunem ca am elaborat o forma a unui algoritm, pentru o problema data, dar nu suntem siguri daca este corecta. Vom testa algoritmul pe un set de date de intrare convenabil alese, folosind metoda de verificare de mai sus. In tabloul respectiv, vom observa daca initializarile sunt corecte, cum se modifica variabilele, cum se termina algoritmul si aceste informatii (in caz ca algoritmul este incorect) sunt foarte utile pentru a realiza modificarile necesare. Practic, intr-un astfel de tablou 'se vede' cum lucreaza algoritmul.
Exemplul 2. Se dau doua matrice A = (ai j) 1 ≤ i ≤ n ,1 ≤ j ≤ m si B = (bi j) 1 ≤ i ≤ n ,1 ≤ j ≤ m cu elemente reale (n ≤ 10, m ≤ 10). Sa se calculeze matricea C = (ci j) 1 ≤ i ≤ n ,1 ≤ j ≤ m , C = A + B.
Datele de intrare ale problemei sunt: numarul de linii (n) si numarul de coloane (m) precum si elementele matricelor A si B. Blocul de citire precedat de marcajul (0) descrie citirea variabilelor de intrare intr-un mod condensat. Sa observam ca, de fapt, citirea celor doua tablouri A si B implica citirea a 2 + 2∙m∙n numere (valoarea lui n, valoarea lui m, cele m∙n elemente ale lui A si cele m∙n elemente ale lui B), deci este vorba tot de un proces repetitiv, analog celui descris mai jos pentru algoritmul propriu-zis (adunarea matricelor). Se convine sa se descrie in acest mod condensat citirea tablourilor pentru a nu complica in mod inutil si pentru economie de spatiu. Cum procedeul de calcul al sumei a doua matrice este bine cunoscut (se aduna elementele de pe aceleasi pozitii), ramane sa analizam, in cele ce urmeaza, modul in care descriem (din punct de vedere algoritmic) acest procedeu foarte simplu.
Sa consideram scrierea uzuala a celor doua matrice:

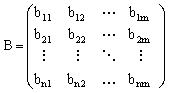
Stim ca se aduna elementele liniei 1 din A cu elementele liniei 1 din B (a11 cu b11, a12 cu b12,.,a1m cu b1m), apoi elementele liniei 2 din A cu elementele liniei 2 din B si tot asa pana la linia n inclusiv. Se observa deci ca se compun doua procese repetitive (primul: se prelucreaza n linii si al doilea: o prelucrare implica m adunari). Pentru descrierea corespunzatoare vom folosi:
o variabila i care sa contina, pe rand, indicii liniilor (1,2,.,n);
o variabila j care sa contina, pe rand, indicii coloanelor (1,2,.,m).
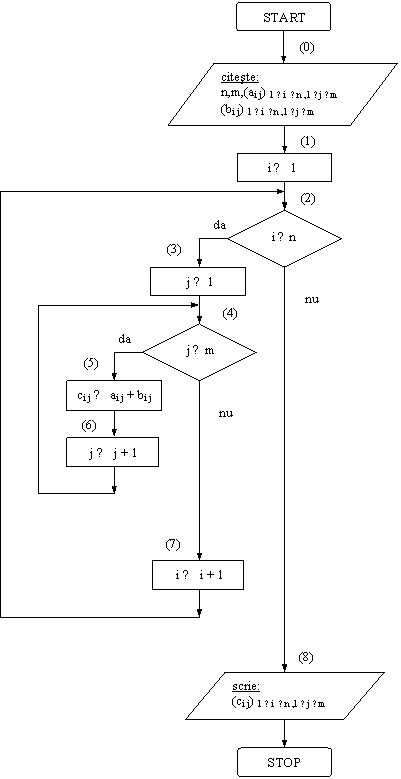
DI: matricele A,B
VL: contorii i, j
DE: matricea C
Urmarind acum schema logica si facand referire la conectorii plasati convenabil, putem descrie cele doua procese repetitive imbricate (al doilea inclus in primul) astfel:
initializeaza i cu 1 (se acceseaza astfel primele linii din A si B);
daca i este mai mic sau cel mult egal cu n, atunci:
initializam j cu 1 (se acceseaza astfel primul element de pe linia i, i fiind acum fixat);
daca j este mai mic sau cel mult egal cu m, atunci:
calculam ci j ca fiind egal cu ai j + bi j;
crestem indicele de coloana cu 1 (trecem la urmatorul element de pe linia i) si salt inapoi la testul (4);
(7) daca j este mai mare decat m, aceasta inseamna ca am prelucrat toate elementele liniilor i din A, respectiv B si trebuie sa trecem la liniile i+1;
daca i este mai mare decat n, aceasta inseamna ca am prelucrat toate liniile si suma este realizata. Urmeaza:
(8) afisarea elementelor tabloului C si Stop.Sa observam ca blocul de scriere din final contine, de fapt, tot o scriere condensata. Este aceeasi conventie, ca si pentru citirea tablourilor.
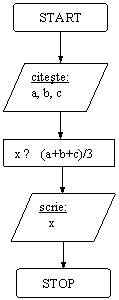
DI: variabilele a, b, c
VL: -
 Este necesara o variabila auxiliara
aux, cu rol de depozit temporar. Prin analogie, pentru a interschimba
continutul a doua pahare (a si b), avem nevoie de un al treilea pahar (aux) in
care, la inceput, sa transferam continutul unuia din cele doua: aux ← a.
In paharul gol (a) aducem continutul celui plin (b): a ← b. In cel ramas
gol (b) aducem continutul celui de-al treilea (aux): b ← aux.
Este necesara o variabila auxiliara
aux, cu rol de depozit temporar. Prin analogie, pentru a interschimba
continutul a doua pahare (a si b), avem nevoie de un al treilea pahar (aux) in
care, la inceput, sa transferam continutul unuia din cele doua: aux ← a.
In paharul gol (a) aducem continutul celui plin (b): a ← b. In cel ramas
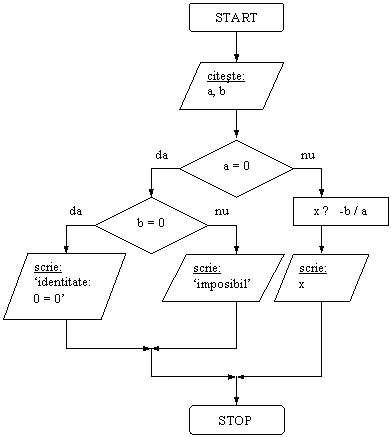
gol (b) aducem continutul celui de-al treilea (aux): b ← aux.Sa se rezolve, in multimea numerelor reale, ecuatia de gradul I: ax+b=0, cu a si b numere reale.
Rezolvare:
Observam ca nu se precizeaza conditia: a ≠ 0. Algoritmul trebuie sa se termine corect pentru orice valori reale ale coeficientilor a si b, ceea ce conduce la analiza descrisa in urmatoarea schema logica.
DI: variabilele a, b
VL: -
DE: variabila x.
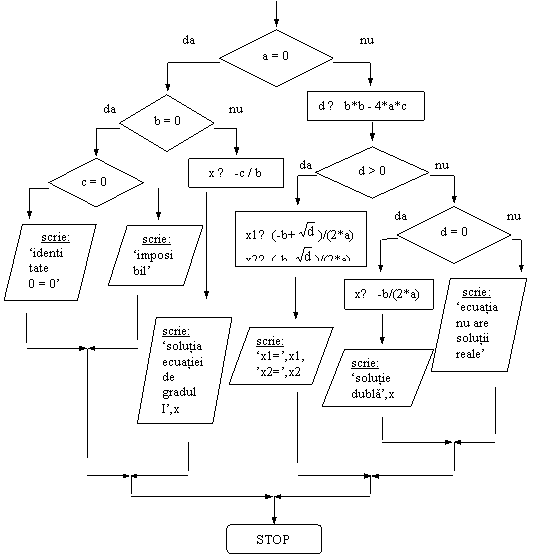
Sa se rezolve, in multimea numerelor reale, ecuatia de gradul al II-lea: ax2+bx+c=0, cu a, b, c numere reale.
Rezolvare:
Este necesara o discutie.
Daca a=0, atunci se rezolva ecuatia de gradul I: bx+c=0.
Daca a≠0, atunci se calculeaza Δ=b2-4ac. Ecuatia are 2 solutii distincte (x1 si x2) daca Δ>0. Ecuatia are o solutie dubla (x) daca Δ=0. Ecuatia nu are solutii reale daca Δ<0.
DI: variabilele a, b, c
VL: variabila d
![]()

da nu
![]()
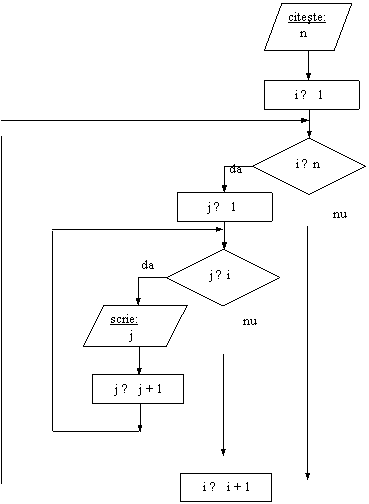
Se da numarul natural n. Sa se afiseze pe monitor n randuri, astfel: pe randul i sa fie numerele naturale de la 1 la i.
Rezolvare:
![]() DI: variabila n
DI: variabila n
![]() DE: contorul j
DE: contorul j
![]()
![]()
![]()
Problema 6
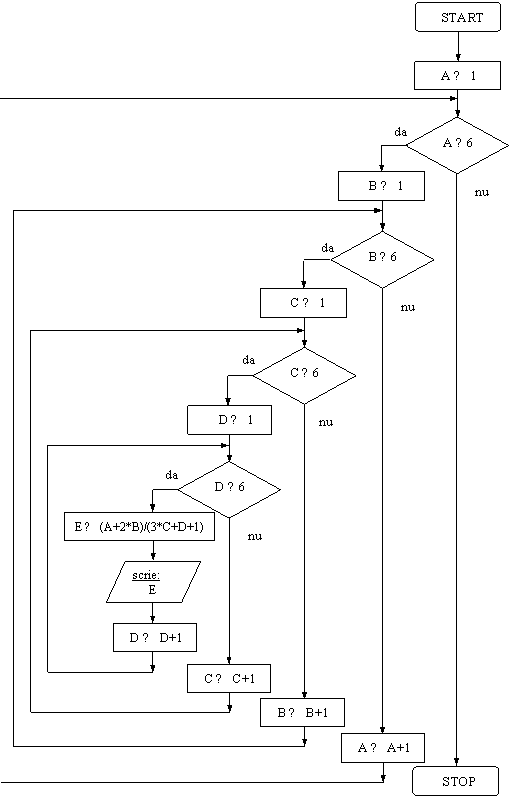 Sa se afiseze toate
valorile posibile ale expresiei
Sa se afiseze toate
valorile posibile ale expresiei ![]() , daca A, B, C, D sunt numere intregi care satisfac: 1
≤ A, B, C, D ≤ 6.
, daca A, B, C, D sunt numere intregi care satisfac: 1
≤ A, B, C, D ≤ 6.
Rezolvare:
VL: contorii A,B,C,D
DE: variabila E
Sa se scrie primii 40 de termeni ai sirului lui Fibonacci.
Rezolvare:
Sirul este definit astfel:
a1=1, a2=1, an+2= an+1+ an pentru n ≥ 1.
Se vor folosi trei variabile pentru calculul termenului curent al sirului: x pentru an,
y pentru an+1 , z pentru an+2.
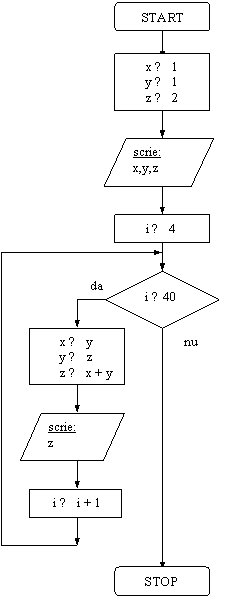 DI: -
DI: -
VL: contorul i, variabilele x, y
DE: variabila z
Observatie. Aceasta solutie foloseste un numar minim de variabile (trei pentru calculul termenilor sirului si variabila contor i pentru numararea lor), dar nu dispunem, la un moment dat, decat de ultimii trei termeni din sir. Daca dorim sa pastram toti termenii calculati ai sirului, este necesar un vector.
Tema. Realizati o schema logica pentru aceasta a doua solutie, cu afisarea tuturor termenilor calculati la final.
Problema 8
Se dau a si b, doua numere naturale nenule. Sa se afle cmmdc(a, b).
Rezolvare:
Solutia I. Calculul celui mai mare divizor comun se va realiza prin algoritmul lui Euclid, al impartirilor succesive. Ultimul rest nenul va fi cmmdc(a,b). Vom observa ce variabile de lucru sunt necesare considerand un caz particular. De exemplu, pentru cmmdc(210,12) realizam urmatoarele impartiri:
D I C R
![]()
![]() 210 = 12 x 17 +
6
210 = 12 x 17 +
6
12 = 6 x 2 + 0
In schema, a reprezinta deimpartitul, b reprezinta impartitorul, iar r reprezinta restul. Catul nu intereseaza. Transferul indicat prin sageti se realizeaza in schema in blocul etichetat cu (1). Se observa ca ultimul rest nenul este pastrat in variabila b.
DI: variabilele a, b
VL: variabila r
DE: variabila b

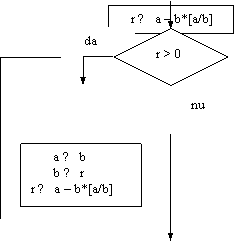
(1)
![]()
![]()


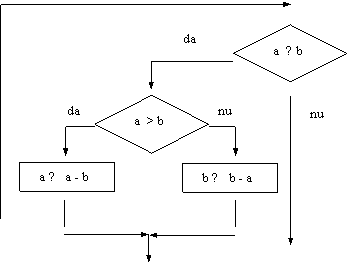
Solutia II. Calculul celui mai mare divizor comun prin scaderi repetate.
Si aceasta schema, ca si cea precedenta, distruge valorile citite ale variabilelor a si b. In finalul schemei, valoarea aflata in variabila a este egala cu cea din b si este egala cu cmmdc(a,b). Daca ulterior calculului celui mai mare divizor comun, sunt necesare valorile variabilelor a si b, acestea se pastreaza in variabile auxiliare.
DI: variabilele a, b
VL: -
DE: variabila a
![]()
Problema 9
Se da n ≥ 4, numar natural. Sa se scrie descompunerea sa in factori primi.
 Rezolvare:
Rezolvare:
DI: variabila n
VL: -
DE: variabilele d, p
Problema 10
Se dau variabila reala x si variabila reala strict pozitiva eps. Sa se afle, in variabila s, valoarea ex cu aproximatia eps.
Pentru calculul aproximativ al lui ex, se foloseste dezvoltarea in serie Taylor a valorii functiei in vecinatatea originii:
![]()
putem scrie:
ex = t0 + t1 +.+ tn + Rn(x) si se demonstreaza ca |Rn(x)| < |tn| pentru 0<2|x|≤ n.
Rezulta ca eroarea eps de calcul aproximativ a valorii lui ex se realizeaza din momentul in care |tn| < eps.
Rezolvare:
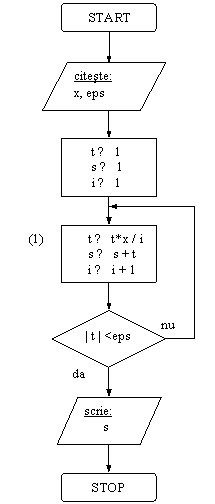 Se foloseste variabila
auxiliara t, in care se va calcula termenul curent al sumei. Observam ca
relatia dintre doi termeni alaturati este:
Se foloseste variabila
auxiliara t, in care se va calcula termenul curent al sumei. Observam ca
relatia dintre doi termeni alaturati este:
tn+1= ![]() deci termenii sumei se
obtin din aproape in aproape si apoi se aduna tot din aproape in aproape.
deci termenii sumei se
obtin din aproape in aproape si apoi se aduna tot din aproape in aproape.
Observam ca in aceasta schema logica nu se cunoaste numarul de repetitii ale blocului (1).
DI: variabilele x si eps
VL: contorul i, variabila t
DE: variabila s
Tema. Realizati o schema logica pentru calculul cu aproximatia eps a valorii functiei sinus intr-un punct x real.
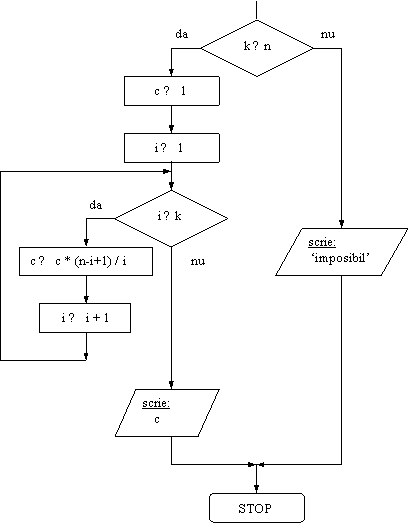
Se dau numerele naturale nenule n si k. Sa se afle, in variabila c,
valoarea ![]() (combinari de n
elemente luate cate k).
(combinari de n
elemente luate cate k).
Rezolvare:
Folosim formula ![]() =
=![]()
DI: variabilele n si k
VL: contorul i
![]() DE: variabila c
DE: variabila c

Problema 12
Se da vectorul a = (ai ) 1 ≤ i ≤ n (n ≤ 10), cu elemente reale. Sa se afle, in variabila s, suma elementelor vectorului.
Rezolvare:
![]() VL: contorul i
VL: contorul i
DE: variabila s

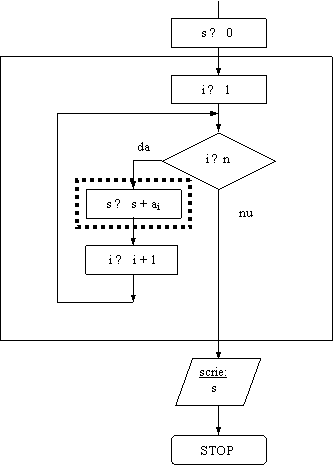
Observatie. In aceasta schema este marcat cu linie subtire grupul de blocuri care genereaza instructiunea repetitiva 'for'. Cu linie punctata groasa este marcata instructiunea care se repeta la fiecare pas.
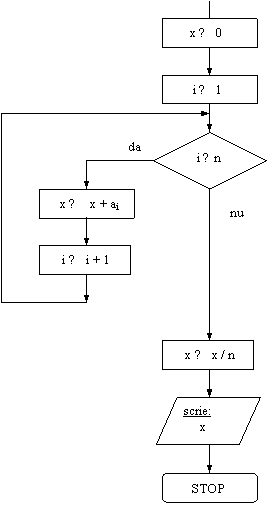
Se da vectorul a = (ai ) 1 ≤ i ≤ n (n ≤ 10), cu elemente reale. Sa se afle, in variabila x, valoarea mediei aritmetice a componentelor vectorului a.
Rezolvare:
![]() DI: vectorul a
DI: vectorul a
![]() DE: variabila x
DE: variabila x

Se da un vector a = (ai ) 1 ≤ i ≤ n (n ≤ 10), cu elemente reale. Sa se afle, in variabila x, norma vectorului a.
Rezolvare:
Stim ca norma vectorului a este ║a║ = ![]() .
.
![]()
Rezulta urmatorul algoritm:
![]() DI: vectorul a
DI: vectorul a
 VL: contorul i
VL: contorul i
x ← ![]()
|

|

|
![]()
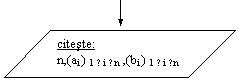
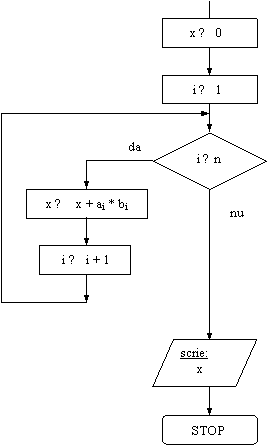
Se dau 2 vectori a = (ai ) 1 ≤ i ≤ n si b = (bi ) 1 ≤ i ≤ n (n ≤ 10), fiecare cu elemente reale. Sa se afle, in variabila x, valoarea produsului lor scalar.
Rezolvare:
Stim ca <a,b>= a1∙b1 + a2∙b2 + . + an∙bn este valoarea produsului scalar.
Rezulta urmatorul algoritm:
DI: vectorii a, b
![]() VL: contorul i
VL: contorul i
DE: variabila x
Problema 16
Se da vectorul a = (ai ) 1 ≤ i ≤ n (n ≤ 10), cu elemente reale. Sa se determine valoarea
x = max (a1,a2,.,an).
Rezolvare:
Variabila x se initializeaza cu a1. Se parcurge apoi vectorul a incepand cu a2 si daca se intalnesc valori mai mari decat x, acestea se trec in x.
DI: vectorul a
VL: contorul i
DE: variabila x

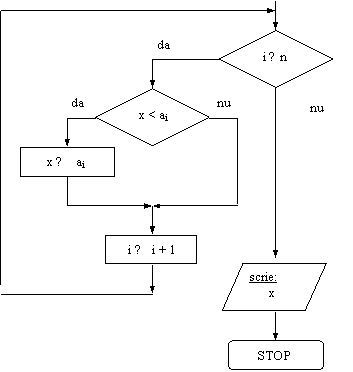
Tema. Realizati o schema logica pentru calculul minimului a n numere si alta care sa determine simultan minimul si maximul a n numere.
Problema 17
Se da vectorul a = (ai ) 1 ≤ i ≤ n (n ≤ 10), cu elemente reale. Sa se afle: in variabila x numarul elementelor pozitive, in variabila y numarul elementelor nule si in variabila z numarul elementelor negative ale vectorului a.
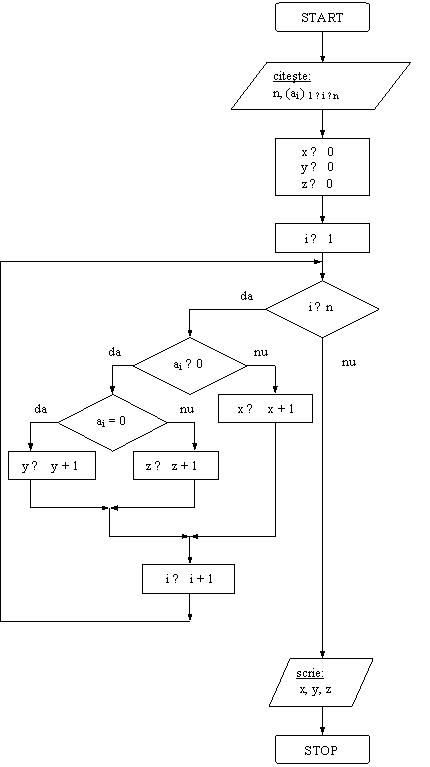
Rezolvare:
VL: contorul i
DE: contorii x, y, z
Problema 18
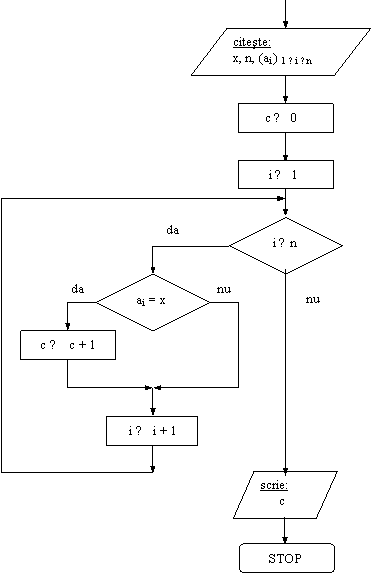
Se da vectorul a = (ai ) 1 ≤ i ≤ n (n ≤ 10), cu elemente reale. Se da variabila x reala. Sa se afle, in variabila c, de cate ori apare x in vectorul a.
Rezolvare:
Variabila c se initializeaza cu 0, deoarece exista cazuri in care ea ramane 0 si dupa incheierea algoritmului (cazurile in care x nu apare deloc in vectorul a). Se parcurge vectorul a, iar contorul c se actualizeaza (prin adaugarea unei unitati) ori de cate ori se gaseste in a un element egal cu x.
DI: vectorul a, variabila x.
VL: contorul i.
DE: contorul c
![]()
Problema 19
Se da vectorul a = (ai ) 1 ≤ i ≤ n (n ≤ 10), cu elemente reale, sortat crescator. Se da x, un numar real. Fara a testa toate elementele vectorului, sa se afle pozitia pe care apare x in vector. Daca nu apare, sa se scrie un mesaj corespunzator.
Rezolvare:
Metoda folosita se numeste cautarea binara. Se noteaza cu li (limita inferioara) si ls (limita superioara) pozitiile intre care se cauta valoarea x (initial li=1 si ls=n). Comparandu-se x cu elementul aflat la egala distanta de li si ls, se poate afla in ce jumatate a intervalului [li,ls] sunt sanse sa fie x; se actualizeaza li sau ls corespunzator, apoi se repeta procedeul pana la gasirea lui x sau pana cand li>ls.
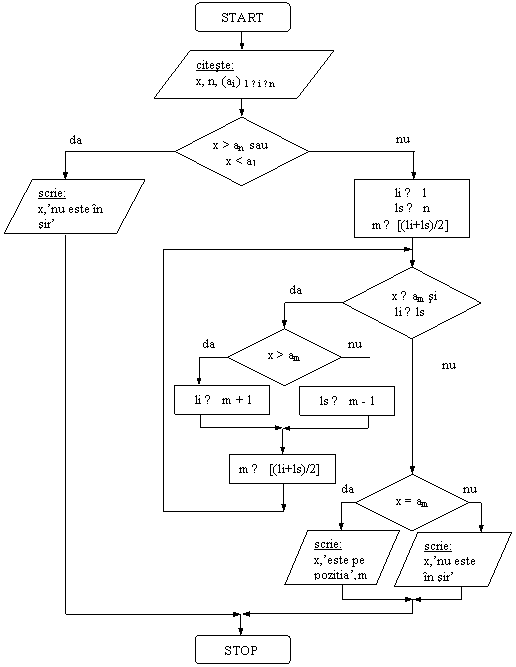
VL: variabilele li,ls
DE: variabila m
![]()
Problema 20
Se da vectorul a = (ai ) 1 ≤ i ≤ n (n ≤ 10), cu elemente reale. Sa se ordoneze crescator acest vector.
Rezolvare: Solutia
I. Metoda folosita se numeste sortare
prin metoda bulelor (bubble-sort) si consta 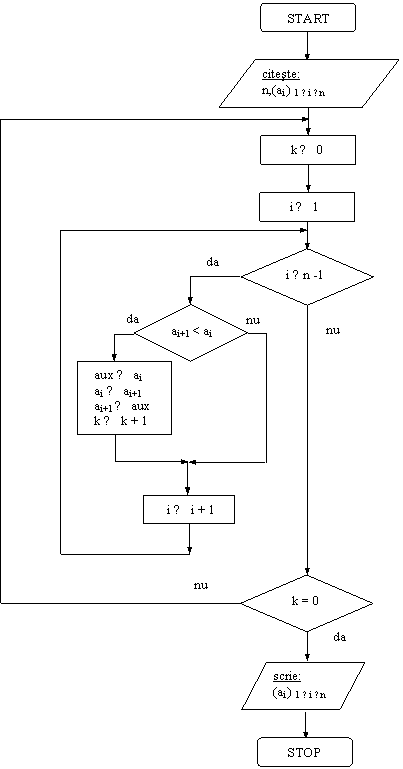 in parcurgerea repetata a
vectorului in scopul compararii elementului curent cu urmatorul si
interschimbarea acestora cand este cazul. Pentru ca algoritmul sa se opreasca,
vom folosi un contor k. Acesta numara cate interschimbari facem la fiecare
parcurgere. Cand ajungem la sfarsitul vectorului si k a ramas 0, inseamna ca
vectorul este sortat.
in parcurgerea repetata a
vectorului in scopul compararii elementului curent cu urmatorul si
interschimbarea acestora cand este cazul. Pentru ca algoritmul sa se opreasca,
vom folosi un contor k. Acesta numara cate interschimbari facem la fiecare
parcurgere. Cand ajungem la sfarsitul vectorului si k a ramas 0, inseamna ca
vectorul este sortat.
DI: vectorul a
VL: contorii i,k;
variabila aux
DE: vectorul a
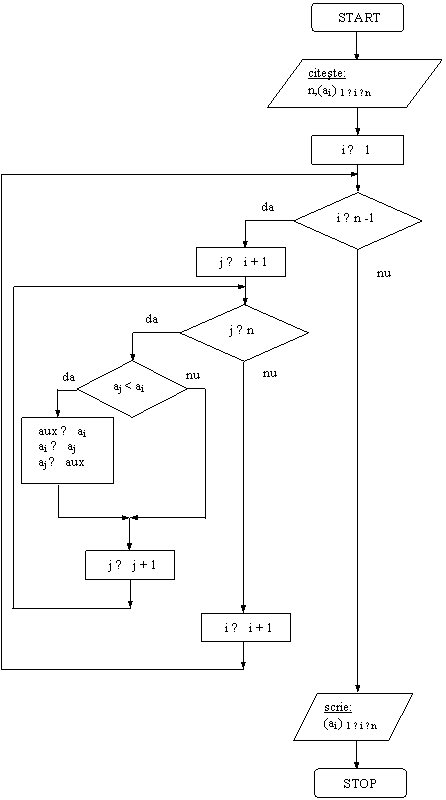 Solutia II. Metoda folosita se numeste sortare prin selectie directa. Pentru fiecare pozitie i, de la
prima pana la penultima, se aduce minimul elementelor a[i], a[i+1], ., a[n] pe
locul i, si acel numar va ramane definitiv acolo. Aducerea minimului se face
prin compararea lui a[i] cu toate elementele de dupa el si interschimbarea
valorilor de fiecare data cand se gaseste un numar mai mic decat a[i]. Este
necesara o variabila auxiliara (aux) pentru interschimbarea variabilelor,
atunci cand este cazul.
Solutia II. Metoda folosita se numeste sortare prin selectie directa. Pentru fiecare pozitie i, de la
prima pana la penultima, se aduce minimul elementelor a[i], a[i+1], ., a[n] pe
locul i, si acel numar va ramane definitiv acolo. Aducerea minimului se face
prin compararea lui a[i] cu toate elementele de dupa el si interschimbarea
valorilor de fiecare data cand se gaseste un numar mai mic decat a[i]. Este
necesara o variabila auxiliara (aux) pentru interschimbarea variabilelor,
atunci cand este cazul.
DI: vectorul a
VL: contorii i, j, variabila aux
DE: vectorul a
Solutia III. Metoda folosita se numeste sortare prin numarare. Se foloseste un vector auxiliar k = (ki) 1 ≤ i ≤ n, ki reprezinta numarul elementelor vectorului a care sunt mai mici decat ai. Se foloseste un vector de iesire b in care se descarca elementele lui a astfel: deoarece sunt ki elemente mai mici decat ai, ai ocupa pozitia ki +1.
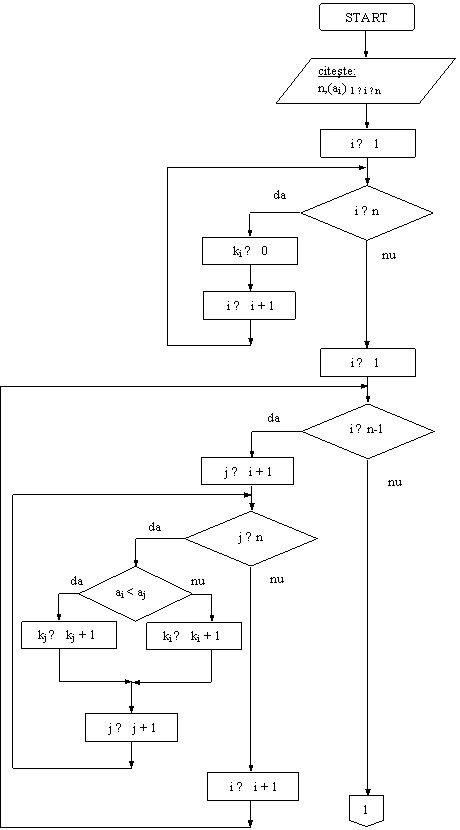
DI: vectorul a
VL: contorii i, j, vectorul k
DE: vectorul b
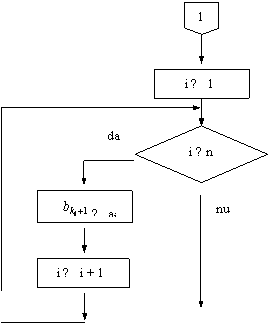

![]()
![]()
Problema 21
Se da vectorul a = (ai ) 1 ≤ i ≤ n (n ≤ 10), cu elemente reale. Sa se transforme vectorul, astfel incat ordinea elementelor sa fie: an, an-1, . a2, a1.
Rezolvare:
DI: vectorul a
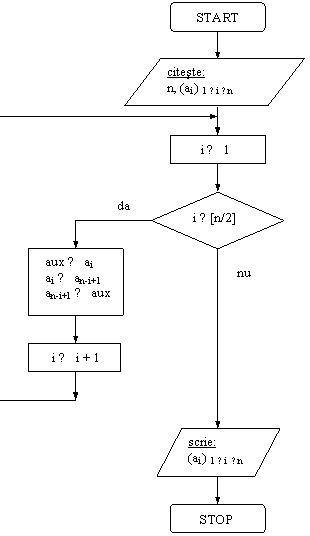 VL: contorul i, variabila
aux
VL: contorul i, variabila
aux
DE: vectorul a
Exemple. 1. Pentru vectorul a = (1 5 3 7 2), unde n=5, deci impar, se vor interschimba 1 cu 2 si 5 cu 7, iar a3 ramane pe loc ([5/2]=2). Rezulta a = (2 7 3 5 1).
Pentru vectorul a = (10 4 2 9), unde n = 4, deci par, exista exact [4/2]=2 perechi ale caror elemente isi schimba locul. Rezulta a = (9 2 4 10).
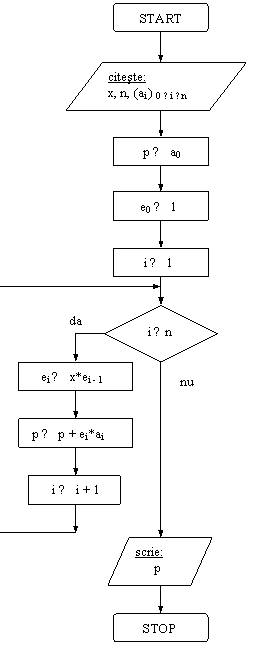
Se dau coeficientii reali ai unui polinom de gradul n (n ≤ 10): a0 , a1,.an-1,an. Se da x real. Sa se afle (in variabila p) valoarea in punctul x a polinomului
P(X)= anXn+ an-1Xn-1+.+a1X+a0.
Rezolvare:
Se foloseste scrierea:
P(X)=(.((anX+ an-1)X+ an-2)X+. a1)X+a0
Exemplu:
3X4-5X3+2X2+9X-5=(((3X-5)X+2)X+9)X-5
 |
nu

![]()
![]()
nu
Solutia II
Se foloseste un vector auxiliar e = (ei) 0 ≤ i ≤ n , calculat cu relatia de recurenta
ei = ei-1∙x, e0 =1 (de fapt ei este xi).
DI: vectorul a, variabila x
VL: contorul i, vectorul e
 DE: variabila p
DE: variabila p
Observatie. Aceasta solutie foloseste vectorul suplimentar e care nu realizeaza nici o imbunatatire a algoritmului (dimpotriva, il lungeste). Solutia I este mai buna decat Solutia II.
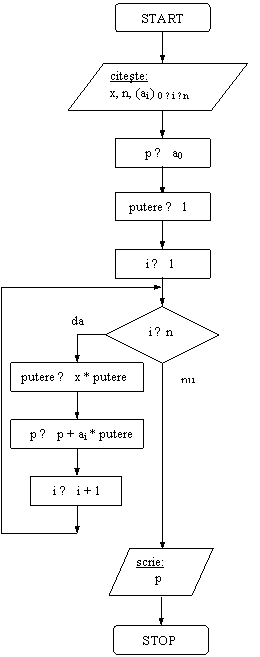
Se foloseste variabila auxiliara putere, in care la pasul i se calculeaza xi. Variabila se initializeaza cu 1 si la fiecare pas valoarea sa se inmulteste cu x.
DI: vectorul a, variabila x
VL: contorul i, variabila putere
DE: variabila p
Se da o matrice patratica A = (ai j) 1 ≤ i ≤ n ,1 ≤ j ≤ n cu elemente reale (n ≤ 10). Sa se afle, in variabila x, suma elementelor de pe diagonala principala.
Rezolvare:
![]() Aceasta suma este a11
+ a22 +.+ ann
Aceasta suma este a11
+ a22 +.+ ann
DI: matricea A
![]() VL: contorul i
VL: contorul i
DE: variabila x

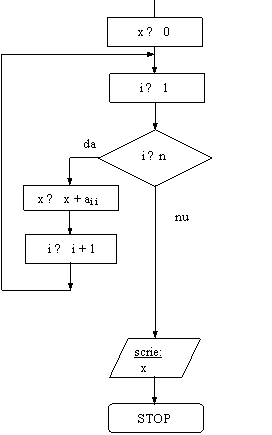
Problema 24
Se da o matrice patratica A = (ai j) 1 ≤ i ≤ n ,1 ≤ j ≤ n (n ≤ 10). Sa se transpuna matricea folosind o singura variabila auxiliara, aux.
Rezolvare:
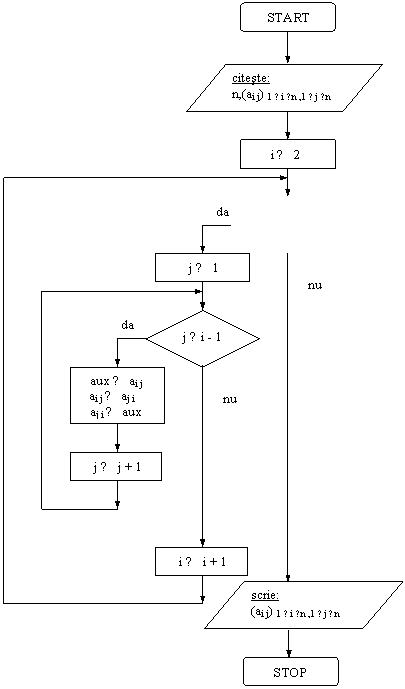 Variabila auxiliara (aux) este
necesara pentru a realiza interschimbarea elementelor ai j si aj
i .
Variabila auxiliara (aux) este
necesara pentru a realiza interschimbarea elementelor ai j si aj
i . DI: matricea A
VL: contorii i, j, variabila aux
DE: matricea A

Se da o matrice A = (ai j) 1 ≤ i ≤ n ,1 ≤ j ≤ m cu elemente reale (n ≤ 10, m ≤ 10). Se da un vector b = (bj ) 1 ≤ j ≤ m, cu elemente reale. Sa se afle daca b este una din liniile lui A.
Rezolvare:
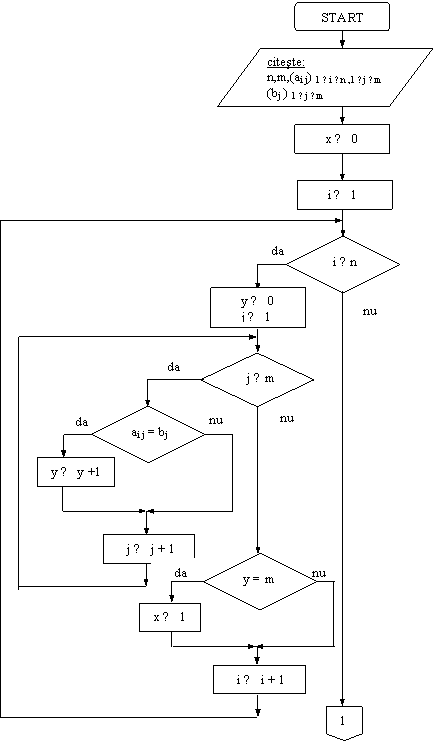 Se foloseste o variabila
indicator x.
Se foloseste o variabila
indicator x.
Ea se initializeaza cu 0 si este modificata daca in
timpul parcurgerii matricei A se gasesc toate
elementele unei linii din A, egale cu cele
corespondente din b. Pentru fiecare linie se numara
in y elementele corespondente egale. Daca y este
m la sfarsitul parcurgerii unei linii, inseamna ca
toate cele m elemente sunt identice cu cele din
vectorul b.
DI: matricea A,vectorul b
VL: contorii i, j, y, variabila indicator x
DE: -
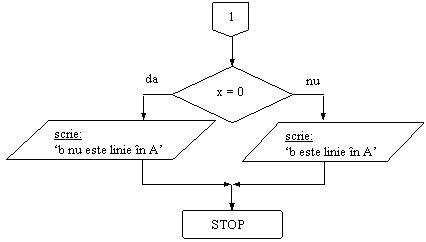
Tema. Scrieti un algoritm care se opreste imediat dupa gasirea primei linii din A, egale cu vectorul b (daca exista o astfel de linie). Algoritmul sa fie de tip structurat.
Se dau doua matrice A = (ai k) 1 ≤ i ≤ n ,1 ≤ k ≤ m si B = (bk j) 1 ≤ k ≤ m ,1 ≤ j ≤ p cu elemente reale
(n ≤ 10, m ≤ 10, p ≤ 10). Sa se afle matricea C = (ci j) 1 ≤ i ≤ n ,1 ≤ j ≤ p , C = A . B.

Rezolvare:
DI: matricele A,B
VL: contorii i, j, k
DE: matricea C
Problema 27
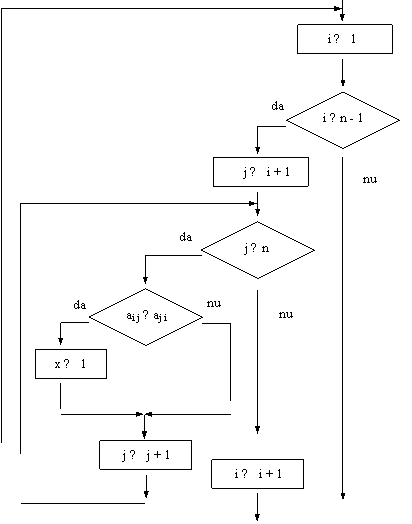
 Se da o matrice patratica
A = (ai j) 1 ≤ i ≤ n ,1 ≤ j ≤ n
cu elemente reale (n ≤ 10). Sa se afle daca A este simetrica fata de
diagonala principala.
Se da o matrice patratica
A = (ai j) 1 ≤ i ≤ n ,1 ≤ j ≤ n
cu elemente reale (n ≤ 10). Sa se afle daca A este simetrica fata de
diagonala principala.
![]() Rezolvare:
Rezolvare:
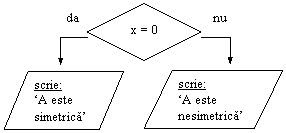
Se foloseste o variabila indicator x.
 Ea se initializeaza cu 0 si este
Ea se initializeaza cu 0 si este
modificata daca in timpul parcurgerii
matricei A se gasesc elemente
![]() simetrice neegale.
simetrice neegale.
DI: matricea A
x ← 0
VL:
contorii i, j, variabila indicator x
DE: -
![]()

|
|