  |
| Politica de confidentialitate |
|
|
| • domnisoara hus • legume • istoria unui galban • metanol • recapitulare • profitul • caract • comentariu liric • radiolocatia • praslea cel voinic si merele da aur | |
Teoria financiara moderna a formalizat un obiectiv complex al gestiunii investitiilor si anume optimizarea corelatiei dintre risc si rentabilitate acestora.
Investitia in active financiare , la fel ca oricare alta investitie, comporta anumite riscuri si anumite rentabilitati pe care evaluatorul trebuie sa le cunoasca . Riscurile investitionale pot fi:
Riscul inflational Riscul inflational este riscul ca moneda sa isi piarda valoarea de cumparare in timp ce preturile cresc;
Riscul unei afaceri Riscul unei afaceri se refera la incertitudinea privind cererea pentru serviciile sau produsele pe care le poate oferi o societate si abilitatea manageriala de a aduce profit companiei;
Riscul optional Riscul apare in momentul necesitatii alegerii unui titlu de valoare dintre mai multe existente; toate aparent potrivite, dar existind posibilitatea ca clientul sa aleaga una cu performante foarte scazute;
Riscul momentului Riscul de a suferi pierderi sau scaderi posibile ale cistigului prin cumparari sau vinzari de titluri de valoare intr-un moment prost ales, in desfasurarea afacerilor societatii;
Riscul pietei Riscul pietei este legat de incertitudinea asupra nivelului viitoarelor preturi datorita schimbarii atitudinii investitorilor. Optimismul sau pesimismul investitorilor poate duce la mari schimbari in pretul valorilor mobiliare, chiar si in cazul unei societati foarte bine cotate;
Riscul creditului Riscul creditului este o masura a valorii creditului societatii emitente. Riscul se refera la posibilitatea ca o societate sa nu poata plati dobinda sau capitalul in momentul in care a ajuns la scadenta;
Riscul solvabilitatii: Solvabilitatea este capacitatea de a converti titlurile de valoare in lichiditati(bani lichizi). Riscul solvabilitatii se refera la modificarile nefavorabile survenite in calitatea titlurilor de valoare cumpar ate initial, aceasta permitind convertirea lor in bani lichizi fara a suferi penalizari sau pierderi importante;
Riscul vandabilitatii Riscul se refera la viteza si la usurinta cu care un titlu de valoare poate fi cumparat sau vindut fara o schimbare majora a pretului. Un titlu de valoare care se gaseste in cantitate mare pe piata si este tranzactionat activ este foarte vandabil si in consecinta lichid;
Riscul schimbarii cadrului legislativ Riscul provine din posibilitatea aparitiei schimbarilor cadrului legislativ sau la nivel guvernamental, care pot afecta valoarea titlurilor cumparate.
Rentabilitatea unei actiuni este determinata de doua componente ale cistigului intr-o astfel de investitie ;dividendul si cresterea valorii de piata. Motivatia investitorului de a cumpara o actiune imediat dupa emisiunea ei este dividendul net pe care il aduce aceasta actiune.Dar orice actiune suscita interesul investitorului si pentru o alta componenta a rentabilitatii si anume cresterea valorii de piata in raport cu pretul de achizitie.Aceasta ultima motivatie este cea care determina o circulatie bursiera mai mult sau mai putin activa a actiunilor in functie de cistigul scontat prin speculatia bursiera.Asadar, rentabilitatea unei actiuni cuprinde dividendul net (D1) si diferenta de curs dintre pretul de piata (P1) si pretul de achizitie (P0) al respectivei actiuni . Deci, rata rentabilitatii unei actiuni se poate determina astfel :
![]()
Aceasta rata a rentabilitatii este definita ca o rata postcalculata. Aceasta formula nu include taxe, impozite si comisioanele ce insotesc fiecare tranzactie financiara.Pornind de la aceasta formula , se pot determina celelalte marimi :
![]()
in care rata rentabilitatii (R) are semnificatia unui coeficient de actualizare a sumei initiale (P0) , pentru a obtine o suma viitoare :
P1+D1=P0(1+R),
In care rata rentabilitatii are semnificatia de rata simpla a dobinzii care ar trebui aplicata unei sume initiale (P0), pentru a obtine la sfirsitul perioadei o suma care inglobeaza dobinda.
P0R=D1+P1-P0
![]()
![]() ,
,
Deci , rata de rentabilitate a unui activ financiar este data de
remunerarea (![]() ) pe care emitentul o poate asigura investitorului de capital
si de cresterea relativa , in timp , a valorii activului respectiv
) pe care emitentul o poate asigura investitorului de capital
si de cresterea relativa , in timp , a valorii activului respectiv ![]() . In termeni concreti
, R reprezinta fructificarea unui leu investit in cumpararea unui titlu
respectiv.
. In termeni concreti
, R reprezinta fructificarea unui leu investit in cumpararea unui titlu
respectiv.
Calculul ex-post al rentabilitatii are numai aplicatii statistice. Un investitor este interesat de rentabilitatea viitoare a titlului pe care il achizitioneaza la momentul t0. Pentru aceasta , calculul rentabilitatii viitoare se bazeaza pe studiul rentabilitatilor individuale intr-o perioada de timp (de exempiu, un an). Seria statistica puate fi compusa din ratele rentabilitatii inregistrate lunar, saptamanal sau la fiecare sedinta. Pe baza frecventelor absolute de aparitie se calculeaza frecventele relative. Pentru a studia speranta matematica de a realiza in vütor o anumita rentabilitate este necesara studierea legii de probabilitate care modeleaza cel mai bine repartitia ratelor de rentabilitate. Numeroasele studii efectuate pe baza unor serii statistice de date au condus la concluzia ca legea de repartitie care aproximeaza foarte blne distributia ratelor rentabilitatii este legea normala. Pe baza acestora, se poate calcula speranta matematica de obtinere a rentabilitatii, prin deterrninarea valorii medii a rentabilitatii individuale,astfel:
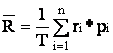 ,
,
unde ri si pi sunt rata rentabilitatii , respectiv probabilitatea de aparitie la momentul i , n este numarul de observatii statistice, iar T este anul in care s-a inregistrat rata anuala de rentabilitate.
Prin riscul unui titlu mobiliar se intelege fie sacrificiul unui avantaj imediat sau absenta unui consum imediat , in schimbul unor avantaje viitoare , fie incertitudinea asupra valorii unui bun financiar inregistrata la o data viitoare.
Riscul este dependent de realizarea posibila a unor evenimente cu grad mare de incertitudine sau aleatorii, care definesc natura si evolutia pietelor financiare si, in particular, ale burselor de valori. Analiza riscului unui titlu rnobiliar face parte din teoria decizie; in conditii de incertitudine, utilizand, in cele mai multe cazuri, calculul probabilistic. Masurarea riscului cu ajutorul probabilitatilor consta in acordarea de grade de adevar cuantificate (adica probabilitati obiective sau subiective dupa caz) tnodificarilor posibile ale valorilor elementelor variabile sau aleatorii, care intervin intr-un calcul global. Aceasta pleaca de la principiul potrivit caruia modificarile determina stari diferite si deci masuratori ale consecintelor (de exemplu: asupra rentabilitatii unei investitii pe piata bursiera). Riscul aferent unei variabile fmanciare poate fi determinat daca se cunoaste distributia probabilitatilor acesteia.
Astfel, pentru a estima riscul ce insoteste profitul care se obtine in urma unui plasament de titluri, trebuie studiate mai intai contributiile tuturor factorilor care influenteaza obtinerea profitului si, ca urmare, stabilirea unei distributii ale probabilitatilor corespunzatoare .Distributia, odata stabilita, va fi analizata, iar pentru aceasta se utilizeaza cel mai adesea urmatorii parametri statistici: media, dispersia si abaterea medie patratica.
Riscul unui titlu mobiliar se poate calcula fie ca dispersia rentabilitatilor seriei dinamice fata de rentabilitatea medie, fie ca abaterea medie patratica a seriei respective, interpretabila ca o crestere sau scadere a rentabilitatii, in functie de valorile (pozitive, respectiv negative) ale abaterilor individuale.
Dispersia se poate asimila cu riscul ca rentabilitatea respectiva sa se abata de la medie.
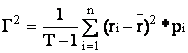
Masura cea mai utilizata a acestei dispersii este abaterea medie patratica.
Abaterea medie patratica este
![]()
unde ri,pi
si ![]() au semnificatia de
rentabilitate individuala , probabilitate de aparitie si rentabilitate medie
.Prin simetria abaterilor posibile in raport cu media se poate admite ca riscul
este masurabil prin valorile negative ale abaterilor, iar rentabilitatea prin
valorile pozitive ale abaterilor.
au semnificatia de
rentabilitate individuala , probabilitate de aparitie si rentabilitate medie
.Prin simetria abaterilor posibile in raport cu media se poate admite ca riscul
este masurabil prin valorile negative ale abaterilor, iar rentabilitatea prin
valorile pozitive ale abaterilor.
Diferiti cercetatori propun semidispersia (semivariance) ca masura a riscului inregistrarii unor abateri negative.Aceste abateri se pot analiza in raport cu media sau, mai bine , in raport cu un anumit prag minim admisibil de rentabilitate (punct mort) care se cere realizat ca o conditie minima acceptabila.
Din analiza seriilor de date bursiere s-a ajuns la concluzia ca distributia cea mai des intilnita in practica prezinta o configuratie simetrica sau normala. Distributia normala este o functie de densitate condusa de legea lui Gauss-Laplace.
In tabelele statistice se pot regasi direct valorile functiei pentru orice valoare data a ratei rentabilitatii .In calculele folosite pentru analiza valorilor mobiliare se apeleaza la legea de distributie normala centrata redusa , de medie 0 si abatere medie patratica 1, definita de relatia :
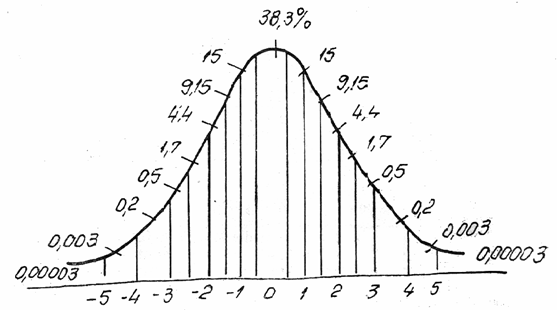
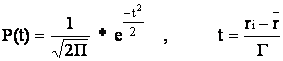
Fig.1 Probabilitatile de aparitie a abaterii medii patratice in functie de multiplicatorii acesteia
Pentru a masura variatia rentabilitatii se recurge la determinarea coeficientului de variatie , calculat dupa formula :
![]()
Acest coeficient masoara intinderea distributiei probabilitatilor de aparitie a ratelor rentabilitatii unui titlu si reprezinta o modalitate de masurare a riscului : cu cit coeficientul este mai mare , cu atit distributia este mai intinsa , abaterea medie patratica este mai mare si rsicul este mai important.
Vom lua ca exemplu cursul actiunii SIDERURGICA HUNEDOARA de la 05.01.1998 pina la 27.02.1998 :
|
DATA |
CURSUL |
VARIATIA |
DATA |
CURSUL |
VARIATIA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
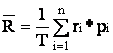 =0,15
=0,15
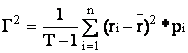 =0,38
=0,38
![]() =0,61
=0,61
![]() =4,066
=4,066
|
PROBABILITATEA |
RENTABILITATEA |
|
|
Minima |
Maxima |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Preocuparea cotidiana a investitorilor financiari si a gestionarilor portofoliilor de titluri este de a anticipa tendintele de crestere sau de scadere ale indicelui general al pietei bursiere. De aceste tendinte este legata evolutia valorii de piata a fiecarui titlu din portofoliu. Fiecare valoare mobiliara urmareste, mai mult sau mai putin, tendintele pietei. Cand indicele pietei este in crestere, majoritatea titlurilor au un curs crescator si invers in perioada de scadere.
Aceasta relatie intre rentabilitatea realizata de o valoare mobiliara si rentabilitatea, ca indice general al valorilor mobiliare, este formalizata in cadrul conceptului de model de piata. Modelul de piata, in forma sa cea mai simpla, reprezinta relatia liniara ce poate exista intre ratele de rentabilitate constatate, intr-o perioada de timp, asupra unei actiuni sau asupra unui portofoliu de valori mobiliare si ratele de rentabilitate realizate in aceeasi perioada, prin indicele general al pietei bursiere.
Surprinderea acestei caracteristici principale a valorilor mobiliare se face prin utilizarea modelului de piata , elaborat de H.Markovitz si dezvoltat ulterior de W.Sharpe.Ideea centrala a acestui model este aceea ca fluctuatiile de curs ale valorilor mobiliare sunt influentate ,in general , de modificarile indicelui general al bursei si , in particular, de modificarile in conditiile specifice ale societatilor emitente ale titlurilor.Astfel , modelul de piata descompune variatia totala a unei valori mobiliare in doua componente :
Riscul sistematic (de piata, nediversificabil) - este legat de variatia principalilor indicatori macroeconomici (PIB, rata inflatiei, rata medie a dobinzii, cursul de schimb) , precum si de alte caracteristici ale tarii emitente a valorii mobiliare respective (situatia politica , riscul de tara, etc.).
Riscul specific - este legat de influenta caracteristicilor specifice fiecarui titlu care se poate descompune la rindul sau in :
a) risc sectorial - risc specific sectorului de activitate de care apartin valorile mobiliare ale emitentului
b) risc specific intrinsec - determinat de modificarile in starea economica a firmei emitente
Relatia dintre rentabilitatea individuala a valorilor mobiliare si rentabilitatea generala a pietei (rentabilitatea indicelui general al bursei) este evidenta .Modelul de piata reprezinta relatia liniara dintre rentabilitatea individuala a titlurilor sau a portofoliului de titluri , pe de o parte , si rentabilitatea generala a pietei bursiere , pe de o alta parte (one-factor model).
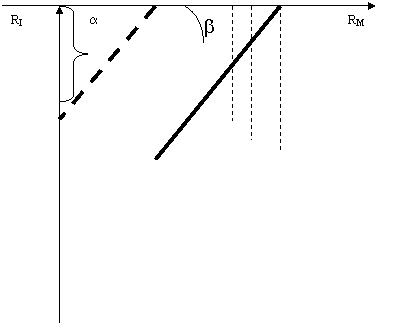
Fig.2 Metoda grafica de trasare a dreptei de regresie
Prin metoda grafica a reprezentarii punctelor de inresectie dintre rentabilitatile titlurilor individuale si rentabilitatea generala a pietei , se determina functia de regresie a acestor variabile. Prin metoda celor mai mici patrate , se pot determina parametrii acestei functi.
Functia care aproximeaza corelatia dintre rentabilitatile titlurilor individuale si rentabilitatea generala a pietei este o dreapta , numita dreapta de regresie.Panta acestei drepte semnifica volatilitatea actiunii, sensibilitatea rentabilitatii actiunii la modificarea rentabilitatii pietei.Imprastierea punctelor de intersectie fata de dreapta de regresie da masura caracterului sistematic sau nesistematic al riscului de variatie a rentabilitatii titlului : cu cit punctele individuale de intersectie se afla mai aproape de dreapta de regresie , cu atit riscul sistematic va avea o pondere mai mare si invers.
Ecuatia dreptei de regresie care , statistic , ajusteaza cel mai bine punctele de variatie este :
![]()
unde Ri - rata rentabilitatii , estimata pentru titlul i
ai - parametru al functiei, egal cu Ri atunci cind RM=0
bi - coeficient de regresie , de volatilitate (beta)
RM - rata rentabilitatii pe piata (indicele general al bursei)
ei - parametru specific titlului i, masoara riscul individual
Cel mai important dintre parametrii functiei de regresie este coeficientul beta , care exprima rentabilitatea marginala a titlului "i" , in raport cu rentabilitatea generala a pietei.
Coeficientul beta se determina pe baza observatiilor asupra rentabilitatilor privind titlul "i" si rentabilitatea generala a pietei.Se calculeaza mai intii cele doua rentabilitati :
![]() si
si ![]()
Aflarea coeficientului beta se face prin metoda celor mai mici patrate , prin egalarea cu 0 a minimului patratelor diferentelor :
![]()
Din calcule rezulta coeficientul beta :
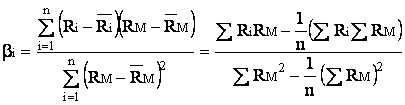
Cu cit coeficientul b este mai ridicat , cu atit riscul sistematic de piata al titlului respectiv este mai mare.
Coeficientul beta se poate determina si prin impartirea covariatiei ratelor rentabilitatii titlului "I" cu cele ale pietei bursiere la dispersia indicelui general al pietei bursiere.
![]()
unde 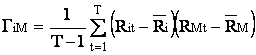 si
si
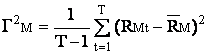
Covariatia
rentabilitatilor pietei bursiere cu ele insele (MM) este
chiar dispersia acestora ![]() , deci beta este egal cu 1"
, deci beta este egal cu 1"
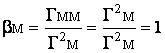
Coeficientul beta al titlurilor individuale exprima deci cantitatea de risc sistematic al titlurilor : de cite ori covariatia rentabilitatii acestora cu rentabilitatea de piata este mai mare decit riscul de piata.
Parametrul alfa al functiei de regresie se obtine din acelasi sistem de ecuatii rezultat prin metoda celor mai mici patrate si utilizat pentru calculul coeficientului beta ;
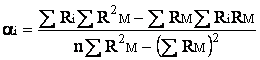
Grafic , parametrul alfa reprezinta intersectia dreptei de regresie cu axa verticala de coordonate si semnifica valoarea rentabilitatii titlului "I" , atunci cind rentabilitatea generala de piata este 0.Parametrul alfa poate lua valori pozitive , negative sau nule , in functie de instabilitatea pietei titlurilor de la o perioada la alta, dar variatia acestui parametru nu prezinta o mare importanta.
Analog se poate descompune riscul unui titlu mobiliar I , astfel:
![]() , determinindu-se astfel cele doua componente ale riscului
unui titlu mobiliar: riscul
sistematic
, determinindu-se astfel cele doua componente ale riscului
unui titlu mobiliar: riscul
sistematic ![]() si riscul specific
(diversificabil)
si riscul specific
(diversificabil) ![]() .
.
Ca exemplu vom lua tot cursul actiunii SIDERURGICA HUNEDOARA , pe o perioada de o luna :
|
DATA |
CURSUL |
VARIATIA |
|
|
Actiunii |
Pietei |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() =1,018
=1,018
![]() =0,9
=0,9
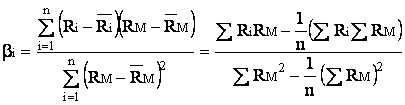 =0,9844
=0,9844
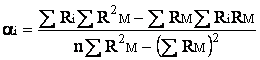 = -0,8304
= -0,8304
Se observa ca actiunea are o rentabilitate medie de 1,018% in perioada 2-27 februarie 1998 , in timp ce rentabilitatea pietei este mai mica , respectiv de 0,9% in aceeasi perioada.
Actiunea Siderurgica Hunedoara are un coeficient beta de 0,9844 ceea ce semnifica faptul ca la o modificare a rentabilitatii pietei cu 1% , actiunea se va modifica cu 0.9844%, o modificare foarte apropiata de cea a pietei.
Deci dreapta de regresie care ajusteaza cel mai bine punctele de variatie este :
![]() =-0,83+0,9844*RM+ei
=-0,83+0,9844*RM+ei
|
|